【摘要】：对于三维波动方程的柯西问题，通常采用球平均法来求解。仿一维波动方程柯西问题的解构造三维波动方程柯西问题的解。应用球坐标系，以点M为球心，at为半径，P为该球面上任意一点，则面积元函数ω在球面（ξ－x）2＋（η－y）2＋（ζ－z）2＝2上的平均值可以表示为故定解问题的解为式称为三维波动方程柯西问题泊松公式。例2.8求解波动方程的柯西问题解ξ＝x＋rsinφcosθ，η＝y＋rsinφsinθ，ζ＝z＋rcosφ
对于三维波动方程的柯西问题（2.103），通常采用球平均法来求解。球平均法的基本思想是引入一个关于u（x，y，z，t）在具有不同球心、不同半径球面上的平均值函数，建立平均值函数所满足的偏微分方程与相应的柯西问题，然后通过平均值函数得到u（x，y，z，t）的表达式：
对于一维波动方程的柯西问题，利用达朗贝尔方法推导了它的求解过程。将一维齐次波动方程达朗贝尔公式解改写成如下形式：
式（2.105）右端两个积分形式相同，令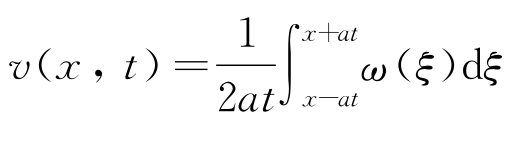
，表示函数ω（ξ）在区间［x－at，x＋at］上的算术平均值。取
则
可验证u1（x，t）和u2（x，t）分别满足定解问题：
因此u（x，t）＝u1（x，t）＋u2（x，t）是定解问题
的解。仿一维波动方程柯西问题的解构造三维波动方程柯西问题的解。应用球坐标系，以点M（x，y，z）为球心，at为半径，P（ξ，η，ζ）为该球面上任意一点，则(www.xing528.com)
面积元
函数ω（x）在球面（ξ－x）2＋（η－y）2＋（ζ－z）2＝（at）2上的平均值可以表示为
故定解问题（2.103）的解为
式（2.111）称为三维波动方程柯西问题泊松公式。
例2.8 求解波动方程的柯西问题
解 ξ＝x＋rsinφcosθ，η＝y＋rsinφsinθ，ζ＝z＋rcosφ
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
