弦振动方程分离变量法的应用

定解问题（2.71）描述了两端固定、仅受初始条件影响的弦的自由振动的物理过程。对于这种既有初值条件又有边值条件的定解问题，采用分离变量法来进行求解：

从物理学知道，一个复杂的振动往往可以分解成许多简单振动的叠加。如弦振动所发出的声音可以分解成各种不同频率单音的叠加。相应于每种单音，弦振动时波形保持不变，从而当时间变化时各点的振幅做同步的变化。也就是说，每种单音都具有形式

这里X（x）及T（t）分别表示仅与x有关及仅与t有关的待定函数。

将式（2.72）代入定解问题（2.71）的方程，得到

整理得到

等式左边仅是t的函数，右边仅是x的函数，左右两端要相等，只有等于同一个常数。记此常数为－λ（其值待定），得到

及

结合边界条件

方程（2.75）的通解分以下三种情况讨论。

（1）λ＜0时，通解为

代入边界条件，可得

由于

只能C1＝C2＝0。故在λ＜0的情况得不到非平凡解。

（2）λ＝0时，通解为

代入边界条件，可得

C1＝0

C2l＝0

因此C1＝C2＝0。故在λ＝0的情况得不到非平凡解。

（3）λ＞0时，通解为

代入边界条件，可得

为了使C2≠0，必须。于是

这样得到了一族非零解

称式（2.81）右端的函数为定解问题（2.71）的固有函数（或特征函数），而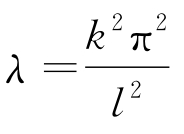称为相应的固有值（或特征值）。

将固有值λk代入方程（2.74）中，可得其通解为

式中，为任意常数。

于是得到定解问题（2.71）的可分离变量的一系列特解：

由于对每一个正整数k都可以找到一个这种形式的解，所以方程（2.83）表示的特解有无穷多个，根据叠加原理，所有特解叠加起来构成一般解

代入初始条件，可得

式（2.85）和式（2.86）右边的两个级数正是初始条件φ（x）和φ（x）在［0，l］区间内正弦展开的傅里叶级数形式，因此，Ak和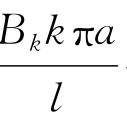分别是φ（x）和φ（x）傅里叶级数的系数，即

将Ak，Bk的表达式代入式（2.84）中，就得到用级数形式表示的定解问题（2.71）的解。

现在证明当定解问题（Ⅰ）初始条件中的函数φ（x）和φ（x）满足一定的条件时，级数式（2.84）确实是这定解问题的解。注意到级数（2.84）中的每一项都满足定解问题（2.71）中的控制方程，因此只要证明在φ和φ满足一定条件时，级数（2.84）可以逐项求导两次就可以。也就是说，如果证明了级数（2.84）求导两次后仍是一致收敛的，那么它一定满足定解问题（Ⅰ）中的控制方程。此时定解问题（2.71）中的初始条件和边界条件的满足也是显然的推论了。

根据傅里叶级数的理论可知：

引理2.1　若φ（x）∈C3，φ（x）∈C2，并且φ（0）＝φ（l）＝φ″（0）＝φ″（l）＝φ（0）＝φ（l）＝0，系数Ak，Bk由式（2.87）和式（2.88）确定，那么级数

收敛。

由引理2.1知，式（2.84）右边关于x及t逐项求导二次以后的级数是绝对且一致收敛的，因而这些求导后的级数收敛于u的相应的导数，所以u满足相应的方程、初始条件及边界条件，故得：

定理2.2　若φ（x）∈C3，φ（x）∈C2，并且

则弦振动方程的定解问题（2.71）的解是存在的，它可以用级数（2.84）给出，其中Ak，Bk由式（2.87）和式（2.88）确定。

通常称条件（2.89）为相容性条件。

当φ（x）和φ（x）不满足定理2.2中所述的条件（例如，φ（x）和φ（x）仅为连续函数）时，可以把φ（x）和φ（x）分别看成函数列(www.xing528.com)

的平均收敛极限。

对应于初始条件为φn（x）和φn（x）的方程的解是

当n→∞时，它平均收敛于式（2.84）所给出的形式解。因此u（x，t）可以作为函数列un（x，t）的平均收敛极限，而un（x，t）的初始条件也分别平均收敛于φn（x）和φn（x）。当n很大时，可以把un（x，t）看成问题的近似解，因为方程及边界条件已经满足，初始条件也近似地得到满足。作为近似解收敛的极限u（x，t），能比所有的un（x，t）更好地反映实际情况。通常也将u（x，t）称为相应初边值问题的解。

例2.6　用分离变量法求下列问题的解：

解　边界条件齐次且是第一类的，令

u（x，t）＝X（x）T（t）

得固有函数

且

于是

由初始条件，得

所以

因此所求解为

解　边界条件是齐次的，令

u（x，t）＝X（x）T（t）

得

及

（2）T″＋a2λT＝0

求问题（1）的非平凡解，分以下三种情形讨论：

①λ＜0时，方程的通解为

由X（0）＝0得

C1＋C2＝0

由X′（l）＝0得

解以上方程组，得C1＝0，C2＝0，故λ＜0时得不到非零解。

②λ＝0时，方程的通解为

X（x）＝C1＋C2x

由边值X（0）＝0得C1＝0，再由X′（l）＝0得C2＝0，仍得不到非零解。

③λ＞0时，方程的通解为

由X（0）＝0得C1＝0，再由X′（l）＝0得

为了使C2≠0，必须，于是

且相应地得到

将λ代入方程（2），解得

于是

再由初始条件得

容易验证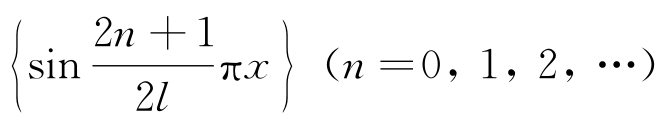构成区间［0，l］上的正交函数系：

利用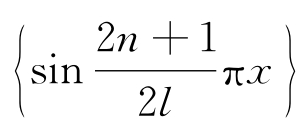正交性，得

Bn＝0

所以