数理方程典型应用案例：非平衡截流子扩散解析

半导体物理学是凝聚态物理学的一个重要分支，是现代微电子材料学与器件学的理论核心。其中，有关非平衡截流子的注入和扩散问题是半导体物理学中的一个重要研究方向。光伏效应的实质是当用适当波长的光照射半导体材料的一侧时，在半导体表面薄层内会产生非平衡截流子。同时，材料内部没有或有较少的非平衡截流子，从而形成从表面到体内的非平衡截流子浓度梯度，进而产生扩散运动，即产生电势差。当粒子浓度分布不均匀时，物质分子将从高浓度区域向低浓度区域转移，直到均匀分布的现象称为扩散。扩散的速率与物质的浓度梯度成正比。

为简化，我们分析一长方体半导体，并假设半导体材料为N型，光吸收仅发生在极薄的表面层（图1.4中的左侧面），则任一截面中粒子浓度相等，故可将该扩散问题看作一维问题进行如下分析。

在N型半导体中，非平衡载流子在无穷小时段dt内通过无穷小长度dx的粒子数dN与非平衡载流子的浓度梯度成正比，即

图1.4　一维截流子扩散示意图

式中，p（x，t）为空穴浓度；Dp为空穴扩散系数；x为空穴扩散方向；负号表示空穴从高浓度向低浓度方向进行扩散。

因此可得在（x1，x2）段内的物体，从t1到t2流入的全部非平衡截流子为

非平衡截流子的流入使物体内部空穴的浓度发生变化，在时间间隔（t1，t2）中，（x1，x2）中空穴浓度从p（x，t1）变化到p（x，t2），其变化量为

非平衡载流子在扩散过程中同时存在非平衡载流子的复合过程，即一边扩散一边复合，因此，在只考虑载流子的扩散运动时，单位体积中浓度的变化应满足方程

式中，等式左边第二项的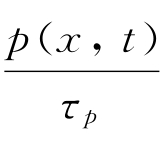表示单位体积中空穴的复合数；τp为空穴的寿命。

假设函数p关于变量x具有二阶连续偏导数，关于t具有一阶连续偏导数，利用格林公式，可以把上式化为

交换积分次序，得到

由于t1，t2及x1，x2是任意的，可得

若半导体是均匀的，则Dp为常数，即得

方程右边第一项为由于扩散引起的单位体积内空穴的积累率。

显然，这是一个一维扩散方程，描述了非平衡截流子的浓度p（x，t）随距离x和时间t的变化规律。

若光照恒定，半导体内部各处空穴浓度不随时间t变化，形成稳定分布，此时称为稳态扩散。非平衡截流子的浓度p只随距离x变化，此时方程变为稳态的扩散方程：

1）确定边界条件(www.xing528.com)

（1）厚度足够大，即厚度w≥扩散长度Lp：非平衡截流子尚未到达样品另一端就全部复合消失，即x＝w时，p（x，t）＝0，此时边界条件为

p（x，t）｜x＝0＝f1（t）；p（x，t）｜x＝w＝0

（2）厚度较短，即厚度w＜扩散长度Lp：非平衡截流子到达样品另一端时尚未全部复合消失，即x＝w时，p（x，t）≠0，此时边界条件为

p（x，t）｜x＝0＝f1（t）；p（x，t）｜x＝w＝f2（t）

就方程形式而言，第（1）种边界条件可看作此边界条件的特例。

（3）厚度较短，即厚度w＜扩散长度Lp，同时在样品另一端抽取非平衡少子，此时边界条件为

（4）如果光吸收发生在一定范围的表面层，则边界条件为

式中，vp为表面复合速度。

以上各式中，f1（t），f2（t）为t≥0的已知函数。如果它们描述的是稳态过程，则上述边界条件中出现的函数与时间无关。

2）求解定解问题

在截流子扩散过程中，由方程与边界条件组成的定解问题主要包括以下两种情况：

（1）由稳态方程分别与边界条件组成稳态定解问题：

该问题均由常微分方程及其定解条件组成，由高等数学知识即可求解，在此不再叙述。

（2）由瞬时方程分别与边界条件组成非稳态定解问题。方程（1）与上述第（2）种边界条件组成非稳态定解问题：

该定解问题中的边界条件为非齐次边界条件，首先须设法利用辅助函数法将边界条件转化为齐次；之后方程若为齐次方程，则可以用分离变量法求解。如果方程为非齐次，则齐次化之后结合分离变量法求解［7］。