蔬菜大棚湿度扩散问题解决方案

蔬菜大棚是一种具有出色的保温保湿性能的框架覆膜结构，其出现使得人们可以吃到反季节蔬菜。一般蔬菜大棚使用竹结构或者钢结构的骨架，上面覆上一层或多层保温塑料膜，这样就形成了一个温室空间。外膜很好地阻止内部蔬菜生长所产生的二氧化碳和水分的流失，使棚内具有可控的生长环境。通过均匀洒水的方式来控制棚内湿度，使得其适合棚内植物生长，求洒水情况下棚内湿度分布情况。

问题假设如下：

假设1：夜晚时，为了保留作物营养、抑制呼吸作用，控制大棚内温度较低，此时蒸腾速率也较低，所以忽略蒸腾作用，且此时为了保温，不进行通风。即只研究白天时大棚内湿度问题。

假设2：大棚面积较大，大棚高度远高于所种的植株高度，即将模型简化为一维的扩散方程，以高度为x坐标建立方程。

假设3：洒水足够均匀，即假设内部水源方程在整个洒水平面上保持一致；为使光利用率达到最高，假设植物被密集种植（可能有梯度，但是此处忽略不计），即植物叶面蒸腾作用在整个平面上保持一致。

假设4：大棚通风只在固定时间段内进行，即平时忽视空气对流以及风速对蒸腾作用的影响；大棚内部，温度可控且保持恒定，即忽视温度对蒸腾作用的影响。

假设5：因为大棚表面覆盖了一层或多层保温塑料膜，假设其水的通透性极差，即不透水。

假设6：水蒸气的传播服从扩散定理，即单位时间内通过单位法向面积的流量与它的浓度梯度成正比，设扩散系数为D，是一个常数。

假设7：植物根部水分充足，即叶面湿度为一个固定常数N1。

由假设1：假设棚内湿度为N（x，t），以白天时间t＝0为起点，地面为x＝0点，大棚高度x＝h为终点，D表示扩散系数，dm1表示在无穷小时间段dt内沿x方向扩散物质的质量，满足

由假设3：假设无穷小时间段dt内沿x方向喷洒的水量为f（x，t），满足

dm2＝f（x，t）dxdt

且此时的洒水方程固定在一个固定平面，即f（x，t）满足

而dt内单位面积上，dx内水分总变化满足

由质量守恒定理可得

dm1＋dm2＝dm3(www.xing528.com)

消去dxdt，假设dx→0，dt→0，可得

假设一天刚开始时，为了尽快升温，排除呼吸作用产生的二氧化碳，做通风处理，所以棚内湿度N等于外界湿度N0，即初始条件为

t＝0：N＝N0

由假设5：

在x＝0处，空气与植物叶面接触，由假设4，即单位面积单位时间内从叶面蒸腾到空气中的水分量只与叶面湿度和近叶面空气湿度之间的差异成正比：

dm4＝k（N－N1）dSdt

其中k为交换系数，与叶面气孔的开合程度相关。

根据扩散定律，

即

为了简便计算，假设此处的k不受时间影响，因为k和D都为正数，所以

式中，。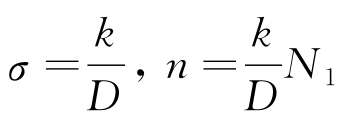

综上，所求解的定解问题为

根据叠加原理，原定解问题分解为

分别采用分离变量法求解定解问题（Ⅰ）和齐次化原理求解定解问题（Ⅱ），然后将两个定解问题的解累加即可得原定解问题的解。