数理方程典型应用案例：维扩散反应问题

假定长为l的细长容器中反应为A→B，并且A和B都在容器中自由扩散，初始时刻A在容器中的分布为N0（x），B在容器中分布为0，即只有反应物A、没有生成物B，边界处与外界无物质交换，求此后A、B在容器中的浓度分布。

考虑反应物A浓度的N在某一小段容器中，由于扩散引起的A的质量变化为

其中D为扩散系数。由于反应在细长容器中进行，为一维扩散反应，

在t1到t2时间段内积分可得

由于反应引起的A的质量变化为

其中k为反应速率和浓度的比例常数。

在t1～t2时间内，x～x＋Δx容器内A的质量改变量为

由质量守恒定律：

利用格林公式，可以将上式化为

由于t1、t2和x范围都是任意的，可以消去积分符号，得

由于D与x无关，可得

以下考虑生成物B的浓度M。

由于反应引起的B的质量变化为

生成物的微分方程为

反应物A的浓度分布满足微分方程定解问题：

生成物B的浓度分布满足微分方程定解问题：

首先求解A的浓度分布。设

N＝ue－kt

则

下面来求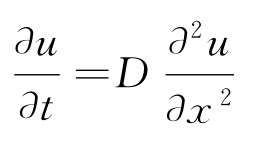的定解问题。

设

u（x，t）＝X（x）T（t）

令(www.xing528.com)

当λ＜0时，

则

所以

C1＝C2＝0

方程无非平凡解。

当λ＝0时，

X（x）＝C1x＋C2

C1＝0，C2取任意值，T′＝C3，若N0（x）－kN＝C3，此解成立，否则此解舍去。

当λ＞0时，

则

所以

将λ代入T的方程得

利用叠加原理构造级数形式的解

将初值代入上式得

利用傅里叶级数得

故

即得反应物的浓度方程。

下面求解B的浓度。运用齐次化原理

令t′＝t－τ，则

其中，f（x，τ）＝kN（x，τ），则

综上

即得生成物B的浓度方程。