无限大平壁导热问题：数理方程典型应用案例及理论分析

厚度为2δ的无限大平壁，导热系数为k，密度为ρ，比热为c，初始时刻平壁与两侧介质温度均为u0，若突然两侧介质温度降为uf并保持不变，使平壁处于冷却状态，设此过程中平壁与两侧介质之间的传热系数为h，求u所满足的方程和定解条件，并求其定解问题。

解　分析这一现象可知，对于无限大平壁，两侧的冷却情形相同，故平壁的温度是对称的，将原点放在平壁的中心。由于平壁无限大，仅考虑沿厚度方向的导热问题，为一维导热问题。

在平壁内沿厚度方向任取一小段Δx，两侧面积为dS，则Δt时间段内从一端流入的热量为

Δt时间段内从另一端流出的热量为

Δt时间段内Δx段温度变化对应的热量为

根据能量守恒

Q3＝Q1－Q2

即

可得

令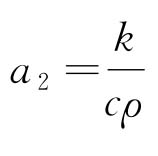，则

定解条件

引入新变量θ（x，t）＝u（x，t）－uf，称为过余温度，则所求解的定解问题变为

采用分离变量法，令θ（x，t）＝X（x）T（t），其中X（x）和T（t）分别表示仅与x和t有关的函数，则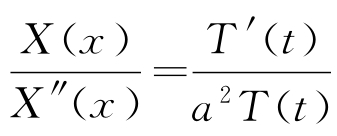，在x和t的定义域内，对于任意x和t均成立，只有两边都等于同一个常数，取作－λ，则

根据边界条件，可得

1）λ＜0

通解为

代入边界条件，可得

即

C1＝C2＝0

故λ＜0没有非平凡解。

2）λ＝0(www.xing528.com)

通解为

X（x）＝C1x＋C2

代入边界条件，可得

C1＝0，C2＝0

故λ＝0没有非平凡解。

3）λ＞0

通解为

代入边界条件，可得

C2＝0

则得

令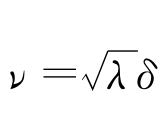，则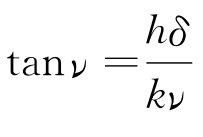，存在无穷多个固有值

及相应的固有函数

T（t）的解为

则

根据叠加原理

根据初始条件，可得

为确定系数Cn，须先证明函数系在［－δ，δ］上正交，设固有函数xi和xj分别对应于不同的固有值λi和λj，即

由于xi和xj都满足边界条件，可得

由于λi≠λj，根据固有函数系的正交性，可得