【摘要】:极值原理可用来描述扩散、传导等现象的热传导方程的重要特性。定理1.1设u(x,t)在矩形RT{α≤x≤β,0≤t≤T}上连续,并且在矩形内部满足热传导方程,则它在矩形的两个侧边及底边上取到其最大值和最小值。换言之,如果以ΓT表示RT的两侧边及底边所组成的边界曲线,那么成立着证明因为将-u代替u,最小值的情形就变为最大值的情形,所以只须考虑最大值的情形。注若u是非齐次热传导方程的解,则仍成立。
极值原理可用来描述扩散、传导等现象的热传导方程的重要特性。对于Ω内的热传导问题,如果物体内部没有热源,物体的边界温度及其初始温度都不超过某值M,则这物体内就不可能产生大于M的温度。
定理1.1(极值原理) 设u(x,t)在矩形RT{α≤x≤β,0≤t≤T}上连续,并且在矩形内部满足热传导方程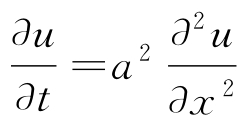 ,则它在矩形的两个侧边(x=α及x=β,0≤t≤T)及底边(t=0,α≤x≤β)上取到其最大值和最小值。换言之,如果以ΓT表示RT的两侧边及底边所组成的边界曲线(通称抛物边界),那么成立着
,则它在矩形的两个侧边(x=α及x=β,0≤t≤T)及底边(t=0,α≤x≤β)上取到其最大值和最小值。换言之,如果以ΓT表示RT的两侧边及底边所组成的边界曲线(通称抛物边界),那么成立着
证明 因为将-u代替u,最小值的情形就变为最大值的情形,所以只须考虑最大值的情形。
以下用反证法证明所需的结论。以M表示函数u(x,t)在RT上的最大值,以m表示函数u(x,t)在边界ΓT上的最大值。如果定理不真,那么M>m。此时在R内一定存在着一点(x*,t*)(t*>0,α<x*<β),使函数u(x,t)在该点取值M。作函数
其中l=β-α。由于在ΓT上
而
V(x*,t*)=M(https://www.xing528.com)
因此,函数V(x,t)和u(x,t)一样,它不在ΓT上取到最大值。设V(x,t)在RT中的某一点(x1,t1)上取到最大值(t1>0,α<x1<β),则在此点应有
因此在点(x1,t1)处,
但直接计算并利用热传导方程可得
这就出现矛盾。它说明原先的假设是不正确的。证毕。
注 若u是非齐次热传导方程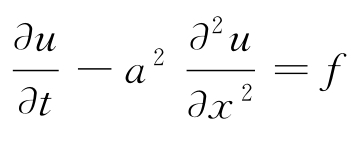 (其中f≤0)的解,则仍成立
(其中f≤0)的解,则仍成立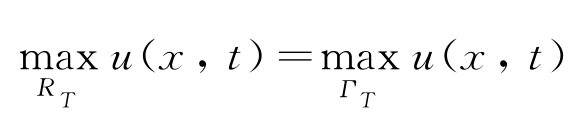 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




