非齐次热传导方程初边值问题的数理方程应用案例及理论分析

在定解问题中，如果微分方程及其定解条件都是线性的，叠加原理同样成立，即如果函数u1（x，t）和u2（x，t）分别是下述定解问题

和

的解，则u（x，t）＝u1（x，t）＋u2（x，t）是定解问题

的解。

定解问题（Ⅰ）可用上节所学的分离变量法求解，对于非齐次线性的求解，一种常用的方法是齐次化原理，其主要特点是化非齐次线性问题的求解为齐次线性问题的求解，然后利用叠加原理得出原问题的解。

由方程的导出过程可知，自由项f（x，t）是由内热源产生的温度的变化，把时间段［0，t］分成若干小段Δtj＝tj＋1－tj（j＝1，2，…，n），当Δtj很小时，在每个小段中，f（x，t）可以看作与变量t无关，用f（x，tj）表示，根据能量守恒定律，可以把这个温度的改变量看作从t＝tj时刻开始的初始温度，它产生的温度变化可以由下面的定解问题来描述：

这个定解问题的解记作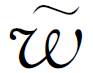（x，t，tj），根据叠加原理，f（x，t）产生的总效果可以看作无数个定解问题（1.45）所描述瞬时效果的叠加，则

即如果记w（x，t，τ）是如下齐次方程定解问题

的解，则

作变换t′＝t－τ，那么定解问题转化为

由前节齐次方程的分离变量法，可得解为

其中

则定解问题（Ⅱ）的解为

综上，得到如下齐次化原理。

齐次化原理［或杜阿梅尔（Duhamel）原理］：若w（x，t，τ）是初值问题（1.46）的解（其中τ为参数），则

就是初边值问题（Ⅱ）的解。将定解问题（Ⅰ）和（Ⅱ）的解进行叠加，可得到定解问题(www.xing528.com)

的解为

其中

例1.4　求解初边值问题

解　由于自由项不依赖于x，t，令u（x，t）＝v（x，t）＋w（x，t），并选择w（x，t）满足

求得

利用上述代换，可得v（x，t）：

由边界条件，可得

由初始条件，可得

于是原问题的解

例1.5　求解初边值问题

解　令，则定解问题转化为

由边界条件，可得

由初始条件，可得

于是原问题的解