定解条件和边界条件在数理方程典型应用案例中的作用

方程（1.10）描述的是物体的温度随时间和空间变化的关系式，没有涉及某一特定导热过程的具体特点，是所有导热过程的通用表达式。给定一个偏微分方程，有通解和特解的概念，通解只要求满足方程及满足某种物理定律，不能完全确定一个物理状态，通解有无穷多个。因此，要完全确定一个物理状态，除了偏微分方程，还需要补充特定条件，这种特定条件就称为定解条件，其通常包括初始条件和边界条件。初始条件是描述该物理状态初始时刻的定解条件，边界条件是描述该物理状态边界上的定解条件。

1）初始条件

对于热传导方程，初始条件表示开始时刻t＝0物体内的温度分布：

式中，φ（x，y，z）为已知函数，它可以是各种各样的空间分布，假如在开始时刻各部分具有相同的温度，则φ（x，y，z）为一常数。

2）边界条件

边界条件表示物体与周围环境之间的热量交换。通常传热问题的边界条件分为以下三类：

（1）第一类边界条件是已知任何时刻物体边界面上的温度值。热传导方程的第一类边界条件又称狄利克雷（Dirichlet）边界条件：

式中，Γ表示物体的边界曲面；g（x，y，z，t）是定义在（x，y，z）∈Γ，0≤t≤T上的已知函数。

（2）第二类边界条件是已知任何时刻物体边界面上的热流密度值，即已知边界面上单位面积单位时间内所流过的热量Q，根据傅里叶导热定律，

实际上相当于已知任意时刻物体边界面上法向的温度变化率的值，即

式中，g（x，y，z，t）是定义在（x，y，z）∈Γ，0≤t≤T的已知函数。(www.xing528.com)

热传导方程的第二类边界条件又称诺伊曼边界条件。如果边界面是绝热的，即边界面上的温度变化率数值为0，则

注意：已知边界面上温度变化率的值，并不是已知物体的温度分布，因为物体内各处的温度梯度和边界面上的温度值都是未知的。

（3）第三类边界条件是将物体放在流动的流体中，物体与周围的流体之间有热交换的情况。在传热学中，依靠流体的流动，将热量从一处传递到另一处的现象，称为热对流。实际上由于流体与边界面之间存在温差，热对流常常伴随热传导。这种物体与流体直接接触时的换热过程称为对流换热，对流换热过程的换热机制既有热对流的作用，也有导热的作用。对流换热的强度通常用表面传热系数来表示，即单位面积上流体与边界面之间单位温差、单位时间内传递的热量。

第三类边界条件就是已知边界周围流体温度u1和边界面与周围流体之间的表面传热系数k1，根据牛顿冷却定律，边界与流体之间的对流换热量为

结合傅里叶导热定律，可得

整理可得

k1及k都是正数，第三类边界条件可以写成

式中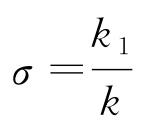，，为已知正数；g（x，y，z，t）是定义在（x，y，z）∈Γ，0≤t≤T的已知函数。热传导方程的第三类边界条件又称罗宾（Robin）边界条件。

在确定某一界面的边界条件时，应根据物理现象本身和边界面的特点给定，不能对同一界面同时给出两种边界条件。