无内热源热传导方程的导出

问题描述：空间静置的某物体G，与周围介质之间有热交换，假定该物体是各向同性连续介质，求物体内的温度u（x，y，z，t）分布。

物理规律：

（1）能量守恒定律。在物体G内任取一闭曲面Γ，它所包围的区域记为Ω，则t1时刻到时刻t2区域Ω所吸收的热量等于该时段内流进此闭曲面的热量。

（2）傅里叶（Fourier）导热定律。物体在无穷小时段dt内沿法线方向n流过一个无穷小面积dS的热量dQ，与物体温度沿曲面dS法线方向的方向导数成正比，即

式中，k（x，y，z）称为物体在点（x，y，z）处的热传导系数，取正值。式（1.1）中负号表示热量总是从温度高的一侧流向低的一侧，与温度梯度的方向相反。

由式（1.1），从t1时刻到t2时刻流进此闭曲面的全部热量为

流入的热量使物体内部温度发生变化，在时间间隔（t1，t2）中物体温度从u（x，y，z，t1）变化到u（x，y，z，t2），需要吸收的热量为

式中，c（x，y，z）为物体的比热，ρ（x，y，z）为物体的密度。根据能量守恒定律

假设函数u（x，y，z，t）关于变量x，y，z具有二阶连续偏导数，关于t具有一阶连续偏导数，利用格林公式，式（1.3）可以转化为(www.xing528.com)

变换积分次序得

由于时间间隔（t1，t2）和区域Ω都是任意的，则

式（1.5）称为无内热源的非均匀的各向同性体的热传导方程，其描述的是物体的温度随时间和空间的变化。如果物体是均匀的，此时k，c及ρ均为常数，记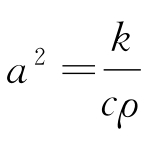，即得

方程（1.6）称为齐次热传导方程。

如果研究对象为薄片的热传导，薄片的侧面绝热，即侧面与周围环境之间没有热交换，可得二维热传导方程

当研究对象是均匀细杆时，假如它的侧面是绝热的、温度的分布在同一截面是相同的，则温度函数u（x，y，z，t）仅与坐标x及时间t有关，可得一维热传导方程

这种含有未知函数偏导数的方程称为偏微分方程。方程中出现的未知函数的最高阶偏导数的阶数称为方程的阶数。如果方程中的项关于未知函数及其各阶偏导数的整体是线性的，就称该方程为线性方程，否则就称为非线性方程。方程（1.7）为二阶线性偏微分方程。