石家庄市空气质量预报与评价

4.1 问题分析

对于问题三，需要利用适当的方法，对问题二中确定的空气质量预报模型的性能进行评价分析。本章以河北省石家庄市为例，利用问题二中建立的模型，以2017年1月、2月气象记录数据为基础，对石家庄市1月、2月的空气质量进行预报，并与真实的空气质量指数进行对比，从而对预测模型结果进行评价。结合数据特点，选取平均绝对误差、平均相对误差、均方差误差和R2四个指标对预测模型结果进行评价。同时，有文献显示，静稳天气指数与空气质量指数之间存在正的线性相关关系，故本文以此作为一种定性的辅助手段，对预测结果进行直观展示。

4.2 模型建立

4.2.1 空气质量指数AQI及计算方法

各项污染物的空气质量分指数（IAQI）中的最大值，即为空气质量指数AQI，当AQI大于50时对应的污染物即为首要污染物。IAQI大于100的污染物为超标污染物。

AQI的计算方法有：一是对照各项污染物的分级浓度限值的浓度限值（GB 3095—2012），API的浓度限值（GB 3095—1996），以细颗粒物（PM2.5）、可吸入颗粒物（PM10）、二氧化硫（SO2）、二氧化氮（NO2）、臭氧（O3）、一氧化碳（CO）等各项污染物的实测浓度值（其中PM2.5、PM10为24小时平均浓度），分别计算得出空气质量分指数IAQI：

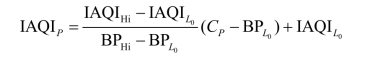
式中：IAQIP为污染物项目P的空气质量分指数；CP为污染物项目P的质量浓度值；BPHi为相应地区的空气质量分指数及对应的污染物项目浓度指数表中与CP相近的污染物浓度限值的高位值；BPL0是与CP相近的污染物浓度限值的低位值；IAQIHi是与BPHi对应的空气质量分指数；IAQIL0是与BPL0对应的空气质量分指数。

其中：CO单位为mg·m-3，其余污染物为μg·m-3；除O3外，所有污染物的浓度限值为24小时平均值；O3浓度限值为日最大8小时平均值，其平均浓度高于800 μg·m-3时，不进行其空气质量分数计算。

表13　空气质量分指数及对应的污染物项目浓度限值

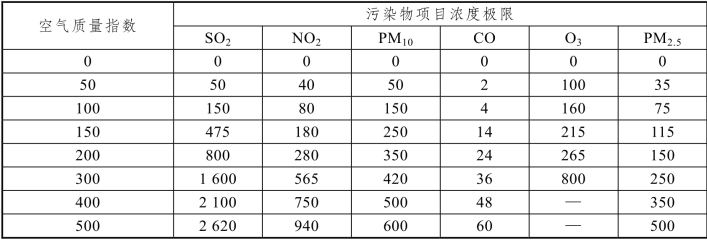
二是从各项污染物的IAQI中选择最大值确定为AQI，当AQI大于50时，将IAQI最大的污染物确定为首要污染物。

式中：IAQI是空气质量分指数；n是污染物项目。

三是对照AQI分级标准，确定空气质量级别、类别及表示颜色、健康影响与建议采取的措施。

4.2.2 静稳指数（SWI）

静稳指数是用于反映大气污染物扩散的综合气象条件。指数越大，大气污染的程度越高。相比单个气象因子，静稳指数是确定各气象因子数据所在阈值，得出权重后，求和得到。因此可以更加全面地反映气象条件对空气质量的影响。

静稳天气形成的主要因素：① 环流因素，如遇大气层结比较稳定，混合层高度降低，就会形成静稳天气；② 地形因素，山地、丘陵、盆地等特殊地貌易阻碍空气流通，污染物不易在水平方向传输扩散。③ 地面风速小，空气中污染物不宜扩散，有利于雾霾形成，容易造成大气污染。其公式表示为

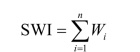
式中：Wi为静稳指数相关因子；i是气象因子的个数。

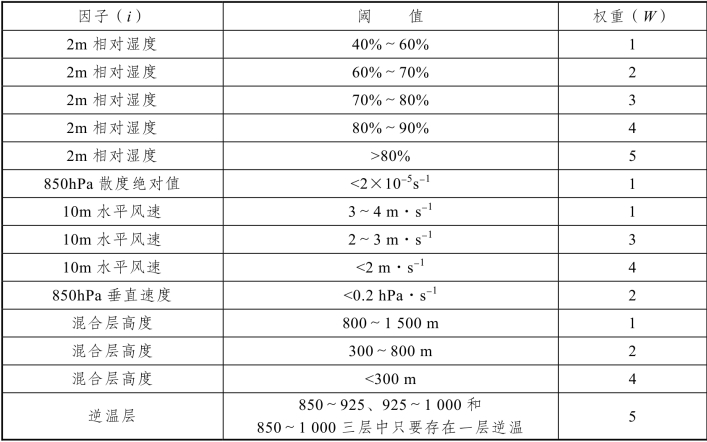
表14　计算静稳天气指数的气象要素、阈值及权重(www.xing528.com)

续表

4.2.3 预测结果评价

基于第二问得出的最佳污染物浓度预报模型的预报结果，使用平均绝对误差和平均相对误差、均方差误差、拟合优度等评价指标，对各污染物的空气质量分指数IAQI、以及综合得出的总体AQI进行拟合检验，另外，还对静稳指数趋势线进行绘图，进一步考察预报模型的预报效果。相关指标的计算公式如下：

（1）平均绝对误差：

（2）平均相对误差：

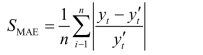
（3）均方差误差：

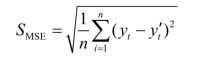
其中：yt是污染物浓度预测值；ty′是污染物浓度监测值。

4.3 模型求解

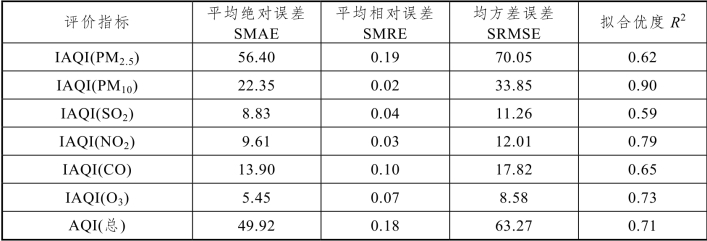
以2017年石家庄1月、2月的天气数据为例，根据第二问所建立的数学模型，对6种污染物浓度进行预测，并计算各污染物的空气质量分指数IAQI及空气质量指数AQI，与根据真实数据计算得到的IAQI及AQI进行对比，从而对模型预报效果进行评价，结果如表15所示。

从表15得出的结果可以看出，AQI的平均绝对误差为49.92，平均相对误差为0.18，均方差误差为63.27，R方为0.71，拟合程度较高，预测结果基本准确。

表15　模型的预测效果

此外，将2017年石家庄市1月、2月的静稳指数数据与AQI绘制在同一张图上（图33），从图中可以看出，模型预报结果与静稳指数具有相同的趋势，与文献中的说法一致。这也说明了本文建立的空气质量预报模型，用RNN神经网络回归分析建立的模型具有一定的实用参考意义。

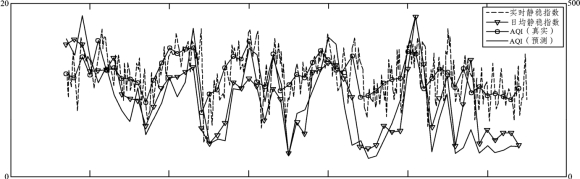
图33　静稳指数与AQI