解决实用数学方法下的非线性污染问题

2.1 问题重述

由于各个城市各季影响因子不同，故不同城市、不同季节、不同污染物的气象因子也不同。通过查找河北省部分城市的相关气象数据，经过初步分析，合理选择建立数学模型，解决能够挑选出与污染物相关性较好的气象因子的适当方法。利用地面风、温度、气压、湿度等基本要素，结合混合层高度、通风量、风切变等中高层和近地面边界层里等参数，对空气质量进行预测分析研究。

2.2 问题分析

鉴于以往对河北空气污染的研究成果，大部分是基于不连续的监测资料且预报模型的建立以线性统计方法为主，而实际情况是空气污染浓度受多种因素影响，在时间和空间上都表现出明显的非线性特征。问题一拟利用近几年最新的连续污染监测资料，在分析河北省石家庄市和邢台市空气污染的时空分布特征的基础上，利用地面和高空资料，研究分析河北空气污染与气象条件的关系，重点探讨降水、大气、天气形势对污染浓度的影响，最后运用SPSS统计软件，利用逐步回归方法对河北省空气首要污染物PM2.5及其他污染物浓度与各气象条件因子的相关关系进行线性回归分析，筛选出与每种污染物显著相关的气象因子。

2.3 模型的建立

1. 多元线性回归分析

多元线性回归模型主要用于研究一个因变量与多个自变量的线性关系。本文利用多元线性回归的方法，对各自变量与因变量的相关关系进行分析。其公式为

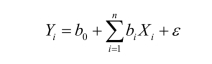
式中：Xi为气象因子；Yi为污染物浓度；0b为常数；ib为回归系数；ε为回归误差。

2. 回归方程的显著性检验

建立了回归方程以后，为了检验回归效果，需要进行统计检验来确定因变量y与自变量x1, x2, x3, …之间是否存在相关关系。

用SST表示因变量的总离差平方和，可以反映y全部数据的离散程度，即

上式可分解成如下形式：

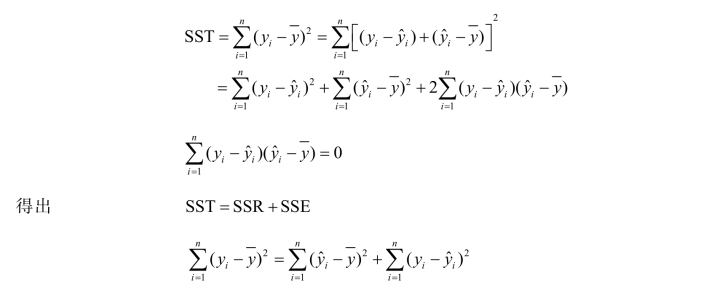
其中：SSE称为残差平方和，是由随机因素和其他未加控制的因素引起的，反映除x以外的其他因素对y的影响大小；而SSR称为回归平方和，是由x和y的线性关系引起的y的取值变化，反映x对y的影响大小。

F-检验法：

3. 逐步回归方法

逐步回归分析是多元回归分析中的一种方法，逐步回归分析建立于线性回归模型的基础上，用于建立最优或合适的回归模型，从而更加深入地研究多个变量之间的相互关系。逐步回归分析，即“最优”子集的变量筛选法，基于偏回归平方和检验逐步引入变量或逐步剔除变量或两者结合，包括向前引入法、向后剔除法与逐步回归法（即逐步回归分析）。

2.4 模型的求解

1. 预报因子的初步选取

在统计分析基础上，建立空气质量预报模型，其准确性取决于预报因子的选取。通过分析污染物浓度与气象环境之间的关系可知，石家庄、邢台市区大气中污染物蔓延扩散、减弱和消失过程的快慢，主要是由当地实时的天气状况、气象条件所决定的。结合本文监测站点给出的大气数据情况，影响污染物浓度的气象条件参数主要有气温、降水、气压、湿度、风速、日照、地表通风系数、混合层高度等。结合日常空气质量预报的经验，首先初步选取有明确物理意义的12个参数作为初选因子，包括：

（1）10分钟风速、日最大风速：反映空气平流输送能力的强弱，通常风速大，空气污染物浓度低；风速小，污染物浓度大。

（2）最高、最低气温，日平均气温：日出前后、日落时分的空气温度，以及当日一天的平均气温，反映城市混合层状况以及逆温状况。

（3）当地日平均气压：反映城市所处的气压场以及大气气压场的变化趋势，通常一天测量四次（2: 00、8: 00、22: 00、24: 00四个测量时间点），取平均值得到。

（4）地表通风系数：反映地面通风风速、湿度和能见度的规律，地表通风系数会影响地面能见度。

（5）20mm等降水量线：反映天气状况及污染物的冲刷情况。

（6）日相对湿度、最小相对湿度：反映大气湿度状况。

（7）一天的日照时数：反映城市天气状况以及污染状况。

（8）混合层高度。

2. 逐步回归方法筛选因子

逐步回归方法是对最优变量进行选择的方法。先用被解释变量对每一个要考虑的解释变量做简单回归，然后以对被解释变量贡献最大的解释变量所对应的回归方程为基础，再逐步引入其余解释变量。经过逐步回归，使得最后包含在模型中的解释变量是最重要的。

四个季节各季的预报因子与污染物浓度的相关系数见表1～表8，分别给出了两个城市的不同污染物、不同季节对应的回归方程。

3. 多元线性回归方程的建立

利用逐步回归方法分别建立多元线性回归方程。将资料中给出的12种气象因子作为预报石家庄市和邢台市区污染物浓度的预报因子，将其输入SPSS软件进行逐步回归预测。对于选取的预报因子，以石家庄、邢台市区为例，采用逐步回归的方法，对2014—2016年三年内的污染物日均浓度，分别分季节进行多元线性回归分析，从而筛选出与污染物浓度显著相关的部分气象因子（分析结果见表1～表8）。

石家庄冬季不同污染物浓度与各气象因子的关系：

PM2.5=0.597X3-0.387X4-0.168X5+0.454X11-0.377X12

PM10= 0.628X3-0.447X4+0.463X11-0.476X12

SO2=0.519X3-0.481X4-0.535X5-0.86X10+0.284X11-0.445X12

NO2 = 0.668X3-0.493X4-0.614X5+0.207X7-0.66X10+0.558X11-0.426X12

CO= 0.618X3-0.474X4-0.287X5-0.235X10+0.54X11-0.325X12

O3 = 0.139X1+0.275X4+0.395X5-0.174X11

表1　石家庄冬季相关气象因子及对应序号

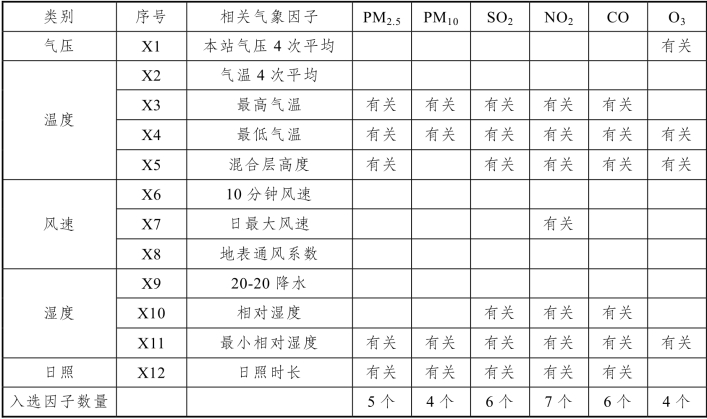
以石家庄冬季的污染物PM2.5为例，12个初始输入的冬季气象因子中，通过逐步回归分析，根据相关性结果，共有5个天气因子即最高气温、最低气温、混合层高度、最小相对湿度、日照时长，与污染物浓度存在良好的相关性。这5个气象因子对应的相关系数分别为0.597, -0.387, -0.168, 0.454, -0.377。其中，最高气温的影响最为明显，其次是最小相对湿度、最低气温、日照时长和混合层高度。同时这也说明了石家庄冬季的污染物PM2.5浓度与气象因子最高气温、最小相对湿度呈正相关，与最低气温、混合层高度、日照时长呈显著负相关。

石家庄春季不同污染物浓度与各气象因子的关系：

PM2.5=-0.211X1+0.570X3-0.699X4-0.262X5-0.267X7-0.332X9+0.325X10-0.209X12

PM10 =-0.165X1+0.839X3-0.765X4-0.265X5-0.332X7-0.287X9-0.317X12

SO2=-0.225X1+0.914X2-1.283X4-0.291X7-0.251X9-0.225X12

NO2 = -0.201X1+0.889X2-1.234X4-0.168X6-0.262X9-0.352X12

CO =-0.331X1+0.424X3-0.879X4-0.573X5-0.257X9

O3 = 0.287X1+1.604X2-0.731X4-0.566X5+0.156X6+0.261X12

表2　石家庄春季相关气象因子及对应序号

石家庄夏季不同污染物浓度与各气象因子的关系：

PM2.5=-0.140X1+0.603X2-0.408X4-0.233X7-0.636X12

PM10= -0.135X1+0.778X2-0.475X4-0.266X7-0.595X12

SO2=-0.183X1-0.225X6-0.203X7-0.631X10-0.209X12

NO2= 0.169X3-0.399X5-0.183X7-0.451X10(www.xing528.com)

CO=0.327X3-0.485X5

O3=0.687X3-0.229X4-0.170X12

表3　石家庄夏季相关气象因子及对应序号

续表

石家庄秋季不同污染物浓度与各气象因子的关系：

PM2.5=-0.354X1+0.868X3-1.197X4-0.423X5-0.263X9-0.408X12

PM10=-0.388X1+1.017X3-1.343X4-0.394X5-0.282X9-0.418X12

SO2=-0.321X1-0.718X4-0.142X7-0.152X9-0.313X11-0.207X12

NO2 = -0.252X1+0.941X3-1.366X4-0.177X5-0.221X9-0.262X12

CO= -0.474X1+0.574X3-1.258X4-0.307X5-0.197X9-0.268X12

O3= 0.141X1+0.790X3-0.127X9

表4　石家庄秋季相关气象因子及对应序号

邢台冬季不同污染物浓度与各气象因子的关系：

PM2.5=-0.269X2+0.599X3-0.166X7-0.133X9+0.527X11-0.33X12

PM10=-0.436X2+0.839X3-0.884X5+0.531X8-0.149X9-0.391X10+0.53X11-0.327X12

SO2=-0.136X1+0.527X3-0.436X4-0.824X5-0.305X7+0.482X8-0.816X10+0.429X11-0.262X12

NO2 = -0.23X1+0.512X3-0.35X4-0.297X5-0.196X9+0.296X11-0.329X12

CO=-0.303X1+0.567X3-0.466X4-0.301X5-0.147X9+0.32X11-0.26X12

O3 = 0.32X1+0.367X2+0.204X7-0.143X11

表5　邢台冬季相关气象因子及对应序号

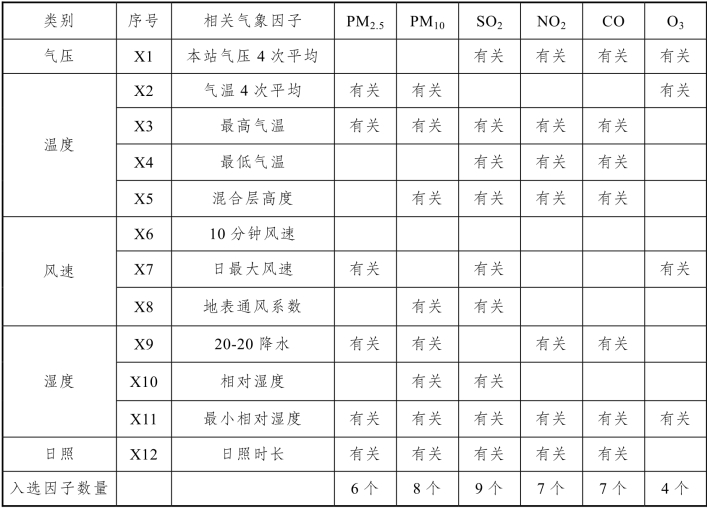
邢台春季不同污染物浓度与各气象因子的关系：

PM2.5=0.608X3-0.699X4-0.981X5-0.242X6+0.887X8-0.182X9

PM10= 0.246X1-0.907X2+1.073X3-0.362X6-0.212X12

S02=0.791X3-0.867X4-1.178X5-0.24X6-0.271X7+1.001X8-0.105X9-0.56X10-0.151X12

NO2= -0.392X1+0.416X3-0.64X4-0.456X6-0.317X7+0.28X8-0.265X9-0.264X12

CO=-0.381X1+0.865X2-1.179X4-0.608X5-0.28X6-0.329X7+0.783X8-0.198X9

O3= 0.581X2-0.196X7+0.167X11+0.309X12

表6　邢台春季相关气象因子及对应序号

邢台夏季不同污染物浓度与各气象因子的关系：

PM2.5=-0.196X1+0.329X3-0.321X6-0.387X12

PM10= 0.542X3-0.172X6-0.304X12

SO2=-0.155X1+0.358X3-0.774X5+0.416X8+0.522X9-0.479X10-0.342X11

NO2=-0.247X1+0.177X3-0.361X6-0.269X11

CO = -0.303X1+0.372X3-0.976X5+0.511X8-0.271X11

O3 = 0.534X3

表7　邢台夏季相关气象因子及对应序号

续表

邢台秋季不同污染物浓度与各气象因子的关系：

PM2.5 =-0.227X1+0.701X3-0.854X4-0.762X5-0.307X7+0.626X8-0.284X9-0.358X12

PM10= -0.247X1+0.798X3-0.927X4-0.324X7-0.289X9-0.603X12

SO2=-0.405X1+0.309X3-0.955X4-0.421X7-0.164X9-0.393X10-0.397X12

NO2=-0.568X1+0.616X3-1.084X4-1.024X5-0.252X7+0.695X8-0.241X9-0.421X10-0.275X12

CO = -0.588X1+0.809X3-1.331X4-0.366X7-0.236X9+0.145X10-0.407X12

O3=0.579X3-0.171X9

表8　邢台秋季相关气象因子及对应序号

4. 相关性检验

逐步回归方程的相关参数如下表所示。石家庄冬季PM2.5的R2为0.519，残差平方和为0.985，置信度F的值为35.224。利用回归方程的显著性检验方法对上述方程进行显著性检验。由F(0.01)(m, n-m-1)分布数值表，可查出F(0.01)(5, 5)=2.7, F(0.01)(PM2.5)=35.224的值远大于F(0.01)(5, 5)=2.7。

表9　逐步回归方程的相关参数

由此可见，本节筛选出的预报因子能够反映大气污染物浓度变化的实际，是合理的。利用同样的方法可对不同城市不同季节的不同污染物进行分析，可以有效筛选出对污染物浓度影响较大的气象因子。