6.1 模型分析
在第二问中,对于网络体系的构建,默认为一级节点之间两两连通,通过改变二级节点与一级节点之间的连接,找出成本费用最低的连接情况。从全局考虑,在第二问的基础上,有如下三个方面可以做出优化:
(1)各节点间地下货物往来的量。为使得各区域交通拥堵系数降至4以下,部分货物需要使用地下运输。第二问采用货物平均的方法,即该地区需要地下运输的货物总量占原来收发货总量的a%时,该区域向其他区域的地下运输货量至少为原计划的a%的量。将需要地下运输的货物平均化。这种地下货物运输的方式有可能并不是最优化的。
(2)两两一级节点之间并不必须相连。一级节点满足要求最少的连接为一级节点之间的最小生成树。最大的连接数为两两接连,应在最大连接数和最小连接数之间选择一个合适的连接数和连接方法。
(3)同一类一级节点下的二级节点之间可以做连线。第二问中,让所有二级节点寻找一个一级节点并与之相连。使得一级节点类中与其二级节点形成了一个深度仅为2的辐射状树。在确定各区域间地下货物往来OD数据表后,若该二级节点通过连接本一级节点下另外二级节点的方式使得成本L降低,可以修改其连接方式。
(4)一二级节点的选择:第一问聚类时,在满足条件的情况且各级节点数目相同时,有多个一级节点和二级节点的选址方案。在聚类出一二级节点之后,之后地下的运输仅为这些节点间的运输。这里引入判别网络优化质量的参数,斯坦纳比(LS(X)/LM(X))。对欧氏平面上的任何有限点集,其最小生成树的长度记为LM(X),斯坦纳最小树的长度记为LS(X),斯坦纳比是判断网络节点优化的一个重要标准。
通过对上述情况的仿真,本文准备采用改变路径和微调节点位置的方法进行优化。本次优化的目标函数是降低成本。
6.2 基于改进-成本目标动态规划的物流网络模型建立
利用植物生长算法对一级节点位置进行优化。采用模拟植物生长算法求解一级节点位置的优化问题,就是将植物的生长环境当作ULS网络的可行域,光源当作全局最优解,模拟真实植物的向光性机理,建立枝叶在不同光线强度环境下向着光源快速生长的动力机制。植物生长算法(PGSA)的目标函数依然为第二问中的成本F,控制变量与生长空间内的所有可能生长点对应,PGSA算法的初始生长点与控制变量的初始值对应。对于变量初始值的选取,必须满足目标函数和限制条件,因此初始点的选取必须在一定范围内。其算法的流程图如图9所示。
基于模拟植物生长算法优化的集体流程步骤如下:
Step1:保留上述节点间的连接方式,将每个一级节点构造为初始的斯坦纳点。
Step2:计算(S1, S2, …, S4)形态素浓度值: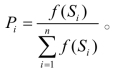
其中f(Si)为与Si相邻边的长度之和;由于P1+P2+…+Pn=1,其概率空间如图10所示,计算机系统不断产生[0, 1]区间中的随机数,这些随机数就像不断向区间[0, 1]上投掷一个小球,小球落在P1, P2, …, Pn的某一概率空间内,这个状态空间所对应的生长点就得到优先生长的机会)。
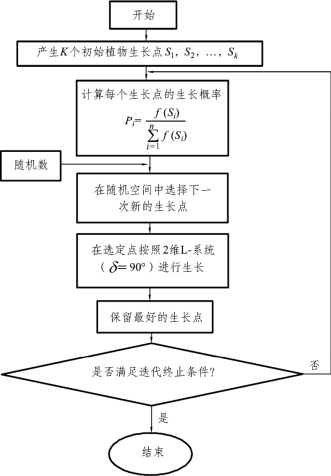
图9 模拟植物生长算法
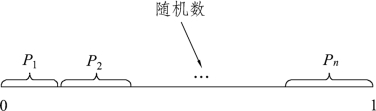
图10 形态素浓度概率空间
Step3:P(i+1)←P(i+1)+P(i), P(i)←P(i)/P(n)。
Step4:if P(i)<random[0, 1]<P(i+1) then F←Si。
Step5:(树枝生长过程)初始状态ω:F。旋转角度:δ=90°。生长规则:F→F[-F][+F]F,树枝分枝后,新生长点为Si(1),Si(2),Si(3)。其中F表示在当前方向上生产节长d,顶点状态变为(x′, y′, α)。其中,x ′=x +dcosα,y ′=y +d sinα。
+:逆时针旋转一个角度δ,顶点的状态变为(x, y, α+δ)。这里,规定逆时针方向为正。
-:顺时针旋转一个角度δ,顶点的状态变为(x, y, α+δ)。
Step6:Si ←min{f (S i),f (Si(1)),f (Si(2)),f (Si(3))}。
Step7:若连续n次迭代无新树枝生长,则植物生长借宿;否则,回到step2。
6.2.1 一级节点内部二级节点连接方式的优化
在第二问中,一级节点内部与二级节点间的连接方式如图10所示(其中n为一级节点,m1, m2, …, m6为二级节点),每个二级节点均与该一级节点相连。若仅考虑n, m1, m2三个点,若m2的货物通过先到m1,再到一级节点n的运输方式(如图12所示)成本比现有的运输成本低(如图11所示),则采用新的运输方式。其判别如下:
因为一二级节点此时均已建成,所以成本仅考虑地下隧道线路的成本和运输成本,在图2变成图3情况下,不光从m2到n的运输方式改变了,同时也大大改善了同一一级节点下二级节点m1与m2之间的货物运输往来,原来m1和m2的货物往来均需要通过n来转运,现在可实现直达。假设该一级节点下属有s个二级节点,实现建立关于该一级节点内部连接状态的矩阵rij(i=0, 1, 2, …, s, j=0, 1, 2, …, s),其中0为该一级节点,若i与j联通,rij=1,不连通则rij=0,则初始化rij的第一行和第一列为1,其余全为0,同时建立距离矩阵D,Dij为从i节点到j节点的地下隧道距离,初始化时Dij也仅第一行和第一列有数据,为一级节点0到各二级节点的欧氏距离。默认为一级节点和二级节点之间隧道均为双同双轨(每条线单向流量为3 600吨)综合分析,步骤如下:
Step1:首先判定m2能否通过m1到达n,若m2与m1连接后,更新m1到节点n的流量qnm1,对qnm1进行判别:

若m2可以通过m1到达n,进行step2。
Step2:计算原来情况的总成本f1(见图10)。
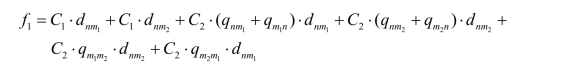
Step3:计算改变连接方式后的总成本f2(见图11)
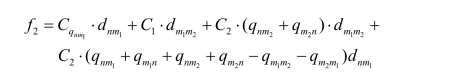
Step4:若f1-f2>0,则自动将节点的连接方式改为如图12所示,即修改m1,m2,n的连接状态,同时更新m2到n点的距离,即dm 2n=dm 2m 1+dm1 n。
Step5:搜索下一节点,重复step1。
若此循环遍历该一级节点的所有二级节点后,可求出最优化成本最小的该类一级节点间二级节点的连接方式。
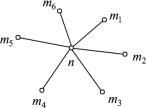
图11
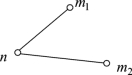
图12

图13
6.2.2 模型的求解(模拟植物生长算法模型的求解)
模拟植物生长算法对一级节点的位置进行优化,其中初始节点的位置分别为问题2中一级节点的位置,在优化节点的同时应保持原有的区域中心点仍处在服务范围内,即max(dni)<4 000。(https://www.xing528.com)
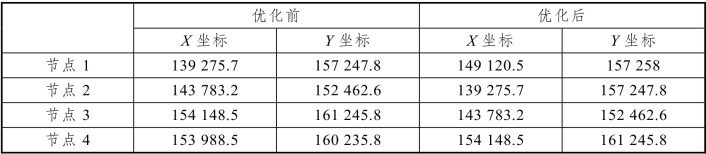
利用MATLAB求解得到优化后一级节点的位置,如图14所示,优化后的坐标见表18。
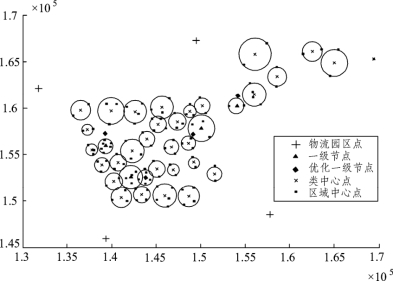
图14 优化位置
表18 优化前后一级节点的位置变化
6.2.3 二级节点连接方式的优化求解
同样利用模拟退火算法对其进行求解,该算法与前面的不同之处在于其成本函数E(x)与连接矩阵不同,上一节中的连接矩阵为32×4的矩阵,用于判定二级节点在哪个一级节点,而本算法中连接矩阵代表二级节点之间相互的连接方式;上一问的E(x)需确保全局的二级节点到一级节点的结果最优,而本算法中成本函数E(x),只用确保本一级节点内达到最优,即
![]()
优化后的结果如图15所示。从图中可以看出,优化后节点之间总的连接数保持不变,而形状由树状变为类似最小支撑树的形状。程序运行结果表明,算法在使得节点内总成本达到最优,即
一级节点1优化前成本1.791 3亿元/年,优化后成本0.721 8亿元/年;
一级节点2优化前成本2.013 5亿元/年,优化后成本0.862 8亿元/年;
一级节点3优化前成本2.630 2亿元/年,优化后成本1.437 6亿元/年;
一级节点4优化前成本2.964 4亿元/年,优化后成本1.126 3亿元/年。
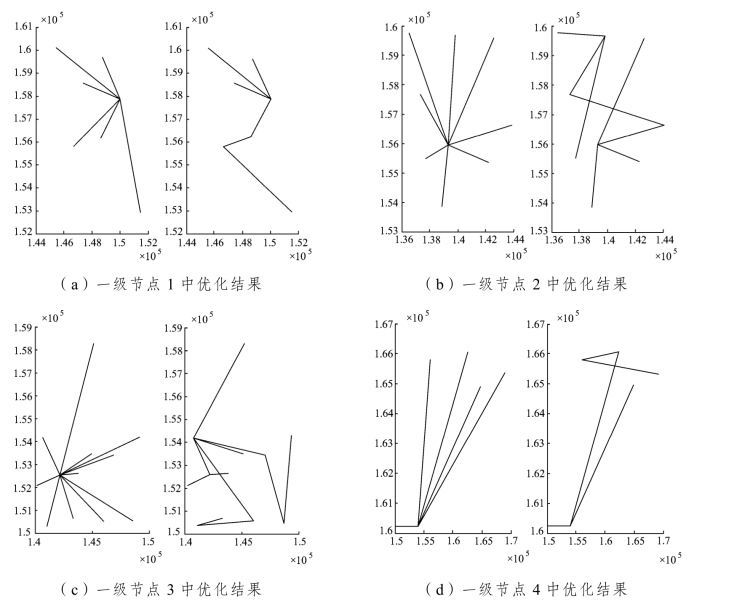
图15 二级节点连接方式的优化结果
6.3 基于增加ULS抗风险能力模型优化
6.3.1 模型建立
上一问中,已经通过改变节点的位置和节点的连接的方式优化的网络。若从抗风险能力如某通道中断和某方向货运量激增考虑,尽量使每个二级节点在一个环上,即通过二级节点一个发现出发,能最终回到该点,这表明该点对于环上任意一点均有至少2条到达路径,这便大大增加了ULS的抗风险能力。在不考虑成本经济因素的前提下,本问便回归到了注明的哈密顿圈问题。假设该一级节点内有s个二级节点,则实质变为了s+1个点的哈密顿圈问题。
约束条件如下:
s+1个节点都需要遍历,故

为了使各级节点连线上的流量尽量符合条件,该一级节点内的货物运输线路应该是多少个圈。假设遍历完所有二级节点的最优路线为m个哈密顿圈。对于每一个节点来说,除一级节点外,只允许最多一条边进入,同样只允许最多一条边出来。可得约束条件:
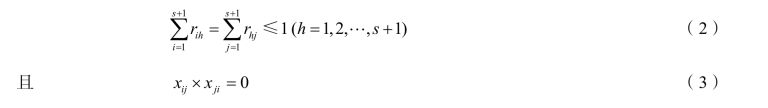
因为是从一级节点0出发的,所以有

该0级节点又是终点,所以有

目标函数为遍历所有节点成本费用最少,同第二问相同。
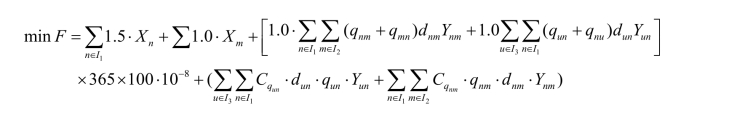
根据题意,在满足约束条件下,需要遍历s+1个节点且用最小的成本。
此时,在第二问USL的基础上,需要将原来已经去除的一级节点和二级节点之间作连接,使得从一级节点出发,在遍历二级节点后能再次回到该一级节点,如图16所示。
6.3.2 模型求解
模型求解如图17所示。
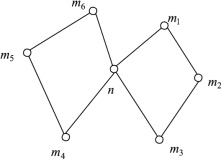
图16 抗风险的USL网络
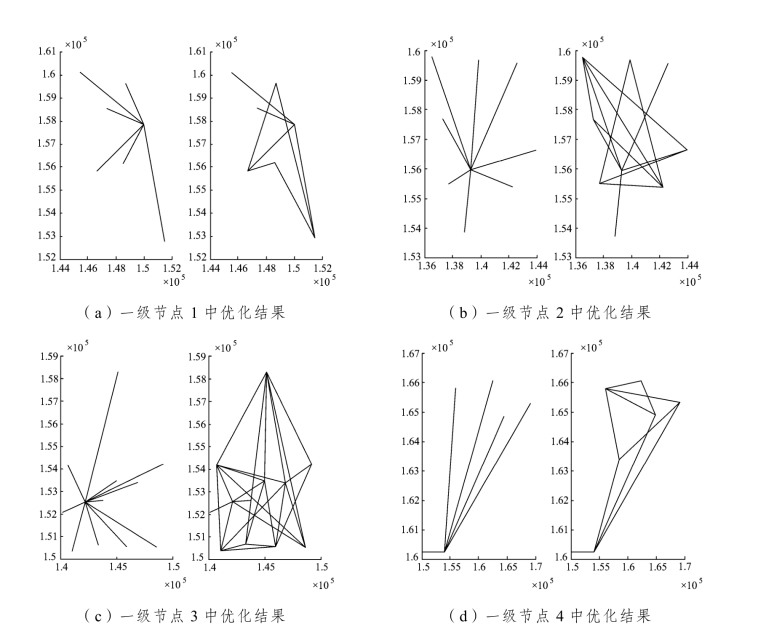
图17 抗风险的USL网络求解
利用模拟退火算法对一级节点内二级节点连接方式进行优化求解,尽量在控制成本的情况下使得成环尽可能多,如图16所示,红色的网络图是优化后的节点连接方式,同时模拟退火算法还给出了优化后的成本,该算法与本节前面不同之处在于其扰动方式与约束条件不同,即
一级节点1优化前成本1.791 3亿元/年,优化后成本0.721 8亿元/年;
一级节点2优化前成本2.013 5亿元/年,优化后成本1.006 2亿元/年;
一级节点3优化前成本2.630 2亿元/年,优化后成本1.630 2亿元/年;
一级节点4优化前成本2.964 4亿元/年,优化后成本1.126 3亿元/年。
优化后的节点连接方式更加复杂,总里程更长,但是成本却下降了,看起来不太符合常理。这是因为本问考虑到资产的折旧,1%的折旧率代表账面资产100年后即为零,而地下网络建设费将以100份平摊到每年的资产流失,所以本例的算法中的目标函数为建设成本乘以1%加上每年的运输成本,最终模拟退火得到该结果。另外,一百年的运输成本与建设成本会不相上下,如果建设时将地下网络修建得密集,有利于两点间不会绕远,运输成本会下降,从长远眼光出发,稍微密集的网络,总成本会更低。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




