【摘要】本文综合运用K-means聚类、目标规划、动态规划等方法,分别建立了基于限定条件的K-means聚类节点选址模型、基于成本目标规划的物流网络连接模型、基于改进-成本目标物流网络动态规划模型以及基于背包问题的物流网络建设时序模型。分别采用模拟退火算法、模拟植物生长算法等进行优化求解,得到了满足交通基本畅通条件下成本最低的优化方案。
对于问题一,首先通过均值化和背包化两种方式对OD数据和交通指数关系进行预处理,得到地下货运量矩阵。进一步对各区域中心点进行一次K-means聚类,通过距离判定和容量判定得到一级节点备选点,确定一级节点后,剔除其样本,进行二次K-means聚类,得到二级节点。最终确定一级节点4个、二级节点32个。
对于问题二,在确定一二级节点位置的情况下,以建造的总成本(包括建设成本和运营成本)为目标函数,采用模拟退火的启发式算法,确定成本F最小情况下的网络连接状况。其成本的目标函数为
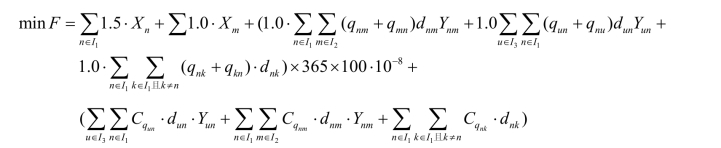
计算得出年均化最小成本为Fmin=13.043亿元/年。
对于问题三,过上述结果进行仿真后,分三步优化网络。首先,应用动态规划优化各一级节点下二级节点的连接方式;其次,优化一级节点间的连接方式;再次,以总成本最低为目标函数,应用植物模拟生长算法重新确定4个一级节点的位置(见图1)。
对于问题四,首先对货运量按照增长(1.0530-1)倍进行近似计算,然后分步按上述模型进行求解,得到一级节点7个、二级节点45个,进一步进行网络连接的模型优化。按照背包问题解法,以年建设里程数为“背包容量”,以各节点实际货运量为“物品质量”进行排序,最终得到8年建设时序图(见图2)。(https://www.xing528.com)
【关键词】K-means聚类;背包化处理;模拟退火算法;模拟植物生长算法
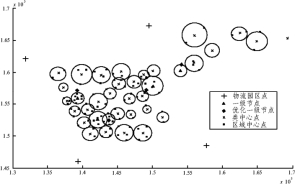
图1 优化位置
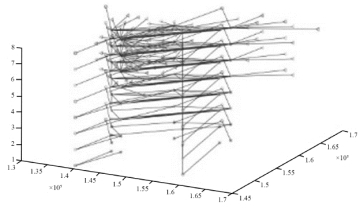
图2 建设时序图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




