3个数学问题的解答-实用数学方法

3.1 对题目一的求解

基因表示之间有很强的相关性，一般认为对于一种肿瘤只有很少的突变基因与其直接相关。题目中给出了关于结肠癌患者与正常人的2 000个基因的数据，需要从这2 000个基因中逐步筛选出与结肠癌直接相关的若干基因。

通过比对数据表中的基因数据，发现有三组共12个基因分别重复，其EST name、GenBank Acc No.以及基因的表达数据均相同。这12个基因的internal id分别为：39、40、41、42；50、51、52、53；260、261、262、263。因此仅保留internal id为39、50、260的3个基因，去除另外的9个分别与之相同的基因数据。故需要处理的基因共有1 991个。

此问同时采用两种算法对1 991个基因数据进行处理：单因素方差分析和巴氏距离分析。结合两种算法的结果，将所有基因分类为信息基因和非信息基因。

3.1.1 模型的建立

同时采用两种算法对1 991个基因数据进行处理：单因素方差分析和巴氏距离分析。

1. 单因素方差分析

单因素方差分析法用于研究一个控制变量的不同水平是否对观测变量产生了显著影响[5]，仅研究单个因素对观测变量的影响。

引入偏方差平方和ST：

误差平方和

效应平方和

在结肠癌例子中，设单个因素（X）为正常人与结肠癌患者的同一某个基因，观测变量则表示某个人是正常人还是结肠癌患者，s是观测变量的个数。

设所给数据中的每一种基因有n组数据，其中有1n个正常人的基因，n2个结肠癌患者的基因。

ST的自由度为n-1，SA的自由度为s-1，SE的自由度为n-s。

在置信水平α=0.02的条件下，查得F0 .02(s-1,n-s)并与F值比较，若F0 .02(s-1,n -s )＞F，则认为该基因是非信息基因，否则认为该基因是信息基因。

2. 巴氏距离分析

巴氏距离（Bhattacharyya Distance）分析是通过构造一个距离函数，代入某个基因数据可求得该基因的巴氏距离值。该值越大，则认为该基因含有更多样本类别信息；反之亦然。

巴氏距离函数为

依据基因所含样本类别信息的多少，将基因分为“信息基因”和“非信息基因”两类。设SI为信息基因集合，SN为非信息基因集合，可对“信息基因”与“非信息基因”做如下定义：

其中：g为基因；B(g)为基因g的巴氏距离；θ为巴氏距离阈值。

3.1.2 模型的求解

通过单因素方差分析法，在可信度为98%（即α=0.02）的条件下筛选出了286个信息基因，详细见附表1（略）。

根据公式（5）各种基因的巴氏距离，得到巴氏距离分布的直方图，如图2所示。各区间基因个数及所占比例如表1所列。

由图2可知，绝大部分基因的巴氏距离小于0.075。这些基因在两个类别中的分布，无论其均值还是方差均无明显差异，可作为非信息基因剔除。

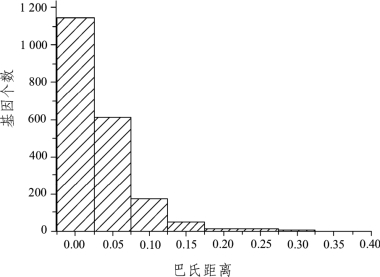
图2　基因巴氏距离分布的直方图

题目提供的基因表达谱中基因巴氏距离的详细分布情况见表1。依据表1和公式（6）对信息基因与非信息基因的定义，可设阈值θ=0.075，并认为上述1 991个基因中有247个基因为信息基因，剩余的基因为非信息基因。这247个基因均在不同程度上包含了样本的分类信息。具体的基因ID等数据见附表2（略）。

表1　各区间基因个数及所占比例

对比单因素方差分析法与巴氏距离分析法所筛选出来的信息基因，单因素方差分析法筛选出286个信息基因，巴氏距离法筛选出247个信息基因。其中有209个基因同时被两种方法筛选为信息基因，重复率达到了84.1%，有效地互相验证了两种筛选方法的合理性。为了避免遗失某些可能的信息基因，我们对两种方法筛选换出来的基因进行合并，最后得到324个基因作为初步筛选的信息基因，其具体的基因数据见附表3（略）。

3.2 对题目二的求解

3.2.1 模型的建立

针对题目二建立了两个模型：特征子集生成模型和基因表达能力测试模型。

1. 特征子集生成模型

特征子集生成模型包含两个子模型：K均值聚类模型[6]、主基因选择模型。

1）K均值聚类子模型

题目一中已经对数据进行了初步筛选，从2 000个基因中筛选出324个与结肠癌肿瘤类型识别相关的信息基因。易知，有2324-1种不同的基因组合，每个基因组合称为一个特征子集。

在此我们采用K均值聚类的方法先对信息基因集合进行处理，设定聚类的个数从2到100不等，聚合表达模式相近的基因。K均值聚类有很多种不同的聚类准则，为避免在选择特征子集时将与该肿瘤类型识别直接相关的特征基因意外剔除，本文选用三种不同的常用聚类准则对信息基因集合进行处理，这三种聚类准则分别为：欧氏距离准则（Euclidean Distance）、皮尔森相关准则（Pearson’s Correlation）、余弦相似度准则（Cosine Similarity）。

（1）欧氏距离准则（Euclidean Distance）。

欧氏距离又称欧几里得距离，将其定义为

（3）余弦相似度准则（Cosine Similarity）。

2）主基因的选择子模型

基因聚类后，每个类别中的基因所包含的信息是相似的，因此可以从每类中选择一个主基因来代表这个类别。该模型选用每类中巴氏距离最大的那个基因作为该类的主基因。

2. 基因表达能力测试模型

该模型采用支持向量机（SVM）作为分类器[7]。SVM常用的核函数有线性核、多项式核、径向基核和S形核。基于径向基核函数（RBF）的优点是可以实现非线性变换。核函数的数量直接影响到模型的复杂性，模型复杂性越高越容易出现拟合问题，而多项式核函数、S型核函数均有比RBF更多的核函数。综上考虑，采用RBF作为SVM的核函数，其具体形式可用数学语言描述为

由于基因表达谱数据样本数目少，为了获得对分类错误率的可靠估计，用两种检验方法对样本类别进行识别：① 在样本上采用留一交叉验证法（Leave-One-Out Cross Validation）[8]进行样本识别。即在样本上每次保留一个不同的样本作为测试样本，其余样本用作SVM的训练样本，重复该过程直到样本中所有样本都被用作测试样本为止；同时记录所有被错误分类的样本数，作为该方法的分类错误数。② 将样本分为训练集和测试集两部分，在测试集上用独立验证法（Hold-Out Method）进行分析，即利用训练集中的所有样本作为SVM的训练样本，对测试集中的样本逐一进行识别；同时记录所有被错误分类的样本数，作为该方法的分类错误数。

在用SVM分类器进行分类的两种检验方法中，独立验证法所得最后验证集分类准确率的高低与原始数据的分组有很大的关系，所以这种方法得到的结果说服性并不强。留一交叉验证法的每一回合中几乎所有的样本皆用于训练模型，因此最接近原始样本的分布，这样评估所得的结果比较可靠；而且验证过程中没有随机因素会影响实验数据，确保验证过程是可以被复制的。将两种验证法同时应用可以有更强的说服力。

综合两种检验方法的识别结果，取错误率最低且维数最小的特征子集作为该聚类方法下的特征基因组。将三种聚类方法下的特征基因组求交集，由此求出与结肠癌肿瘤类型识别直接相关或认为有较强相关性的特征基因组合。

3.2.2 模型的求解

首先，分别采用上述三种不同聚类准则，对初筛选得到的324个基因数据进行K-means聚类。聚类的个数设定为2到100，分别得到99组，共297组聚类结果。

然后运用“特征子集生成模型”，分别对这三种聚类准则聚类产生的聚类结果进行处理，得到3×99=297个特征子集。采用欧氏距离准则的K-means聚类所得主基因internal id、采用皮尔森相关准则的K-means聚类所得主基因internal id以及采用余弦相似度准则的K-means聚类所得主基因internal id，见“附件\去噪前数据\1.xls”、“附件\去噪前数据\2.xls”、“附件\去噪前数据\3.xls”（略）。

得到特征子集后，用“基因表达能力测试模型”对其进行SVM识别。图3～图5表示每种不同准则的K均值聚类所得的特征基因子集，因K值变化而得到的支持向量机识别结果。

图3　采用欧氏距离准则聚类所得特征基因子集的分类能力

图4　采用皮尔森相关准则聚类所得特征基因子集的分类能力

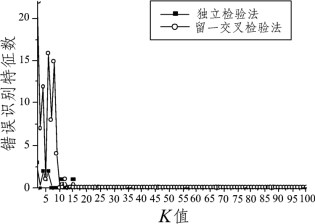
图5　采用余弦相似度准则聚类所得特征基因子集的分类能力

由图可知，三者均在K=10时，两种检验法的支持向量机分类能力达到最佳，即误分率都为0。当K=10时，三种不同聚类准则的聚类所得的特征基因子集见表2。

表2　最佳分类效果的特征基因子集

对三个聚类准则对应的三个特征基因子集取交集，所得到的基因组合是特征基因组合。最终获得6个特征基因，其internal id分别为：493, 625, 1 042, 1 668, 1 671, 1 750。筛选出的特征基因及其描述见表3。

表3　结肠癌肿瘤类型识别特征基因及其描述

(www.xing528.com)

3.3 对题目三的求解

基因表达谱不可避免地含有数据噪声，这会给数据处理带来不良影响。故建立降噪模型，对数据进行先期降噪是非常必要的。此处的降噪大致可分为两类：一类是剔除大量的“无关基因”，即非信息基因；另一类是尽可能降低制作基因表达谱时带入的系统测量误差噪声。在上文第一问中，实际已建立了第一类降噪模型，进行了数据处理。故本部分主要解决的是第二类降噪问题。

在使用小波包降噪方法时，有一些参数是需要人为设定的。比如小波函数的选择、小波包分解层数等，因此需要对各参数不同组合时的降噪效果进行评价。本文建立了“图像信噪比估计模型”，对各参数组合的小波包降噪效果进行量化对比。以此为依据，选择降噪后效果最佳的灰度图像像素值矩阵，作为下一步筛选特征基因的数据。

3.3.1 模型的建立

本文建立的降噪模型的算法流程如图6所示。

图6　信息基因原始数据的降噪模型

由图可知，信息基因原始数据的降噪模型由三个子模型构成：信息基因原始数据与二维灰度图像的映射模型、基于小波包变换的软阈值降噪模型、图像信噪比（SNR）估计模型。下面对它们进行分别阐述。

1. 信息基因原始数据与二维灰度图像的映射模型

为了便于计算机处理和图像降噪方法运用，我们采用一种映射模型将信息基因原始数据转化为二维灰度图像。该映射模型将信息基因原始数据矩阵看作二维图像，样本各基因的表达值分别映射为图像中某序列点的灰度值。这样数据矩阵转换成以基因表达值为灰度的数字图像，同时保留了原来数据的全部信息。映射模型表达如下：

令I(x,y)为图像中点(x,y)的灰度，则

其中：zmax, zmin分别对应信息基因表达值矩阵中z的最小值和最大值。

由式（10）可知，对信息基因原始数据作灰度转换的同时，也对所有数据进行了归一化处理，在一定程度上亦可消除系统误差的影响。

2. 基于小波包变换的软阈值降噪模型

1）小波包定义

显然，μ0(t)和μ1(t)分别为尺度函数和母小波函数，即小波包由小波进一步推广得到。对小波子空间再进行二进细分可得

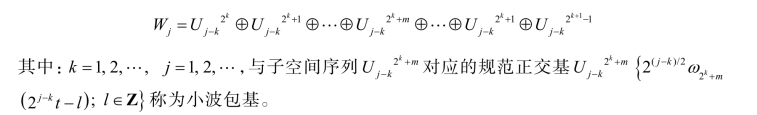
2）基于小波包变换的软阈值降噪算法

一般认为，某个信号对应的小波系数包含有该信号的重要信息，其幅值较大；而噪声对应的小波系数是一致分布的，个数较多，但幅值较小。基于这一思想提出软阈值和硬阈值去噪方法，即在众多小波系数中，把绝对值较小的系数设为零，而让绝对值较大的系数保留或收缩，分别对应于硬阈值和软阈值方法，得到估计小波系数；然后利用估计小波系数直接进行信号重构，达到去噪的目的。选用的阈值公式为

其中：σ是噪声的标准方差；n是信号的采样长度。

基于小波包变换的软阈值降噪算法如下：

（1）图像的小波包分解。选择一个小波并确定小波分解的层次N，对图像进行N层小波包分解。

（2）确定最佳小波包基，即对于一个给定的熵标准，计算最优小波包基。

（3）小波包分解系数的阈值量化，对于每一个小波包分解系数，选择一个适当的阈值并对系数进行间值量化。

（4）小波包重构，根据第N层的小波包分解系数和经过量化处理的系数，进行图像的小波包重构。

本文所建模型选用香农（Shannon）熵标准，采用不同类型小波和不同小波分解层次，分别对转化后的灰度图像进行降噪。

3. 图像信噪比（SNR）估计模型

信噪比，即SNR（Signal to Noise Ratio），其计算公式为

式中：S表示原始信号的强度；N表示原始信号受污染后的信号中所包含的噪声强度。由此可知，若原始信号未知，要计算受污染信号的信噪比是有困难的。因此要对信噪比进行估计[9]。

本文建立的图像信噪比估计模型，使用了局部均值和局部标准差的概念。首先将图像分割成很多小的子块；然后计算这些子块的标准差作为局部的噪声大小，并选择包含子块数最多区间的局部标准差的平均值作为整个图像的最佳噪声估计。具体操作步骤如下：

（1）将图像分割成多个4×4, 5×5, …, 8×8的小块，计算每个子块的局部均值LM和局部标准差LSD：

式中：Si为图像子块第i个像素的灰度值；N为图像子块的像素总数。均匀的图像子块，其局部标准差较小；而包含边缘或纹理的不均匀子块，其局部标准差较大。计算出整幅图像所有子块的局部标准差，并找出其中最大和最小的局部标准差值。

（2）在最大和最小局部标准差值之间建立若干个等间隔的区间，并按照每个子块局部标准差值的大小将其列入相应区间，将包含块数最多的那个区间局部标准差的平均值作为整幅图像的噪声值。

（3）将所有像素点灰度值的均值与估算得到的噪声值之比作为整幅图像的信噪比。

3.3.2 模型的求解

运用子信息基因原始数据与二维灰度图像的映射模型，对324个信息基因、62个样本的基因运用该模型进行处理，得到62×324灰度图像，如图7所示。

图7　灰度转换图像

运用基于小波包变换的软阈值降噪模型对灰度转换图像进行降噪处理。在处理过程中，选用香农（Shannon）熵标准，以及两种常用的小波函数：4阶Symlet小波（sym 4）函数、2阶Daubechies小波（db 2）函数，分别进行1～4层小波包分解，对灰度转换图像进行降噪处理。各处理结果如图8、图9所示。

图8　1～4层小波包分解软阈值降噪处理结果图（采用4阶Symlet小波函数）

图9　1～4层小波包分解软阈值降噪处理结果图（采用2阶Daubechies小波函数）

运用图像信噪比（SNR）估计模型分别求解各处理结果图像的信噪比SNR。各处理结果图像的信噪比SNR值如图10所示。

图10　各处理结果图像的信噪比SNR

由图10可知，当小波包分解层数为2并采用2阶Daubechies小波函数，对原数据的灰度图像进行小波包软阈值降噪处理时，效果最佳。

采用上节筛选出的最佳降噪处理结果灰度图像的数据，运用本文建立的特征基因筛选模型，重新对特征基因进行筛选。采用欧氏距离准则的K均值聚类所得的主基因internal id、采用皮尔森相关准则的K均值聚类所得的主基因internal id，以及采用余弦相似度准则的K均值聚类所得的主基因internal id，见“附件\去噪后数据\1.xls”、“附件\去噪后数据\2.xls”和“附件\去噪后数据\3.xls”（略）。

图11～图13为采用不同准则的K均值聚类所产生特征子集的分类能力。

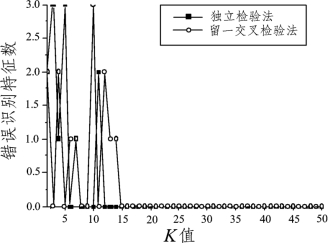
图11　采用欧氏距离准则聚类所得特征基因子集的分类能力

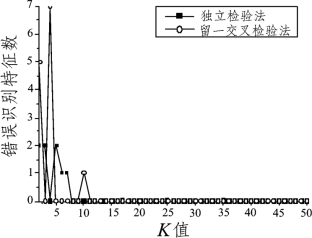
图12　采用皮尔森相关准则聚类所得特征基因子集的分类能力

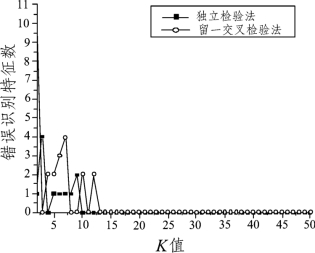
图13　采用余弦相似度准则聚类所得特征基因子集的分类能力

最终筛选出的特征基因及其描述见表4。

表4　降噪后筛选出的结肠癌肿瘤类型识别特征基因及其描述

将这些基因同降噪处理前选出的特征基因进行对比：降噪处理前选出的6个特征基因包含了降噪处理后选出的4个特征基因，而Hsa.3306和Hsa.1454这两个基因未出现在降噪处理后选出的特征基因集合中。

由此可以看出，降噪处理在一定程度上去除了系统测量误差，使得在提取基因表达谱信息时，提取到的信息能更加准确。

3.4 对题目四的求解

图14为融入了先验信息的特征基因筛选模型。其中：虚线部分表示聚类时筛选出所有包含先验基因的基因组合。

对于已有的先验信息，为避免先验基因被剔除、确保所筛选特征基因的准确性，模型在进行K均值聚类时，可按照以下思路对本文已建立的筛选模型进行更改：

首先筛选出所有包含先验基因的基因组合，再对所选出来的基因组合进行表达能力测试，最后进一步筛选得到新的特征基因。

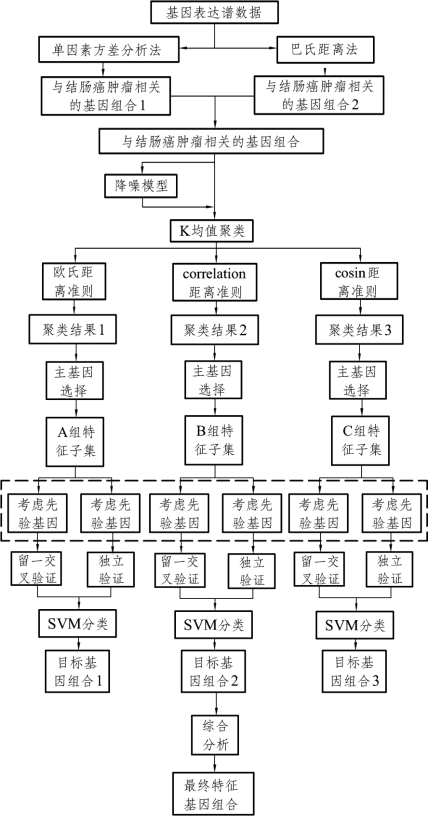
图14　融入先验基因的特征基因筛选模型