模糊综合评价法在实际应用中的例子

例1（优秀科技成果的评选） 设有甲、乙、丙三项科研成果，有关资料见表9.5.1，现欲从中评出一项优秀成果。

表9.5.1　三项科研成果的有关情况

设评价指标集为U={科技水平，实现可能性，经济效益}，设评语集为V={高，中，低}或{大，中，小}。在专家们讨论、统一认识后，得到评价指标的权系数向量为

专家评价的结果见表9.5.2。表中的数字是指赞成此种评价的专家人数与专家总人数的比值。这样就得到模糊评价矩阵

表9.5.2　专家评价结果

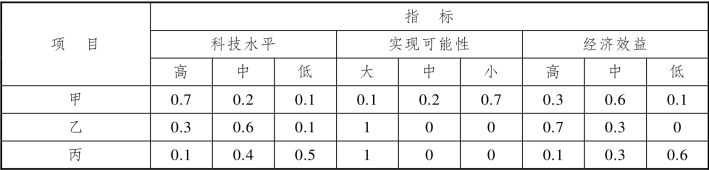
利用模型M(∧,∨)进行合成，于是三项科研成果的综合评判结果为

从评价结果中可以看出，乙项科研成果应评为优秀项目。

例2（某部门员工的年终评定关于考核的具体操作过程） 以对一名员工的考核为例，见表9.5.3，根据该部门工作人员的工作性质，将18指标分成工作绩效（U1）、工作态度（U2）、工作能力（U3）和学习成长（U4）这4个子因素集。

表9.5.3　员工考核指标体系及考核表

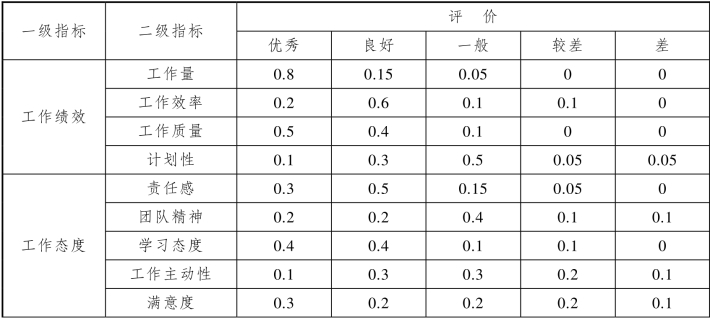
续表

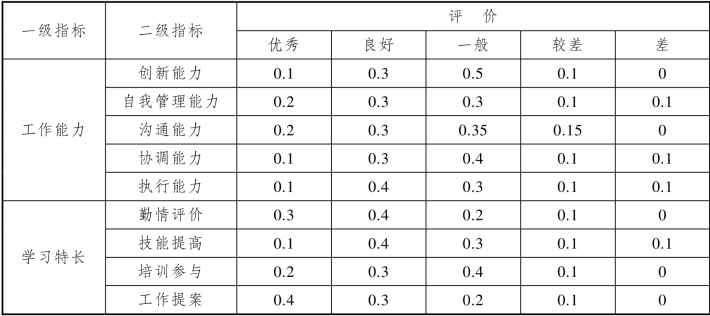(www.xing528.com)

设专家设定指标权重，一级指标权重为

二级指标权重为对各个子因素集利用模型M(·,+)进行一级模糊综合评价得到

利用模型M(·,+)运算B=A◦R，进行二级综合评判为

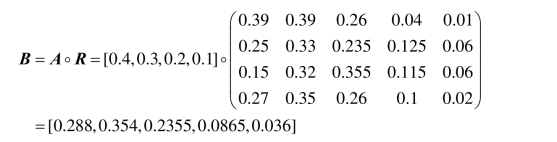
MATLAB程序如下：

clc, clear

a=load（'mhdata.txt'）; %把表中的原始数据保存在纯文本文件mhdata.txt中, mhdata.txt中数据附在本节末。

根据最大隶属度原则，认为该员工的评价为良好。同理可以对该部门其他员工进行考核。

以上说明了如何用综合模糊评价来解决企业中的人事考核问题，该方法在实践中取得了良好的效果。经典数学在人事考核的应用中显现出了很大的局限性，而模糊分析很好地将定性分析与定量分析结合起来，为人事考核工作的量化提供了一个新的思路。

文件mhdata.txt数据：