神经网络模型求解及实用数学方法

神经网络常用模型共70多种，具有代表性的有：感知器、多层前馈（BP）网络、Hopfield网络（优化）、Boltzmann机（在BP中加入噪声）、双向联想记忆网络（快速存储）。下面我们简单介绍感知器和BP神经网络。

1. 感知器

感知器（Perceptron）也叫感知机，是美国计算机科学家Frank Rosenblatt于1957年提出的一种神经网络模型。早期的研究人员试图用感知器模拟人脑的感知特征，但后来发现感知器的学习能力有很大的局限性，以致人们曾经对它的能力和应用前景得出了十分悲观的结论。尽管如此，这种神经网络模型的出现对后来神经网络模型的出现产生了极大的影响。单层感知器的结构与功能都非常简单，以至于在解决实际问题时很少采用，但由于它在神经网络研究中具有重要意义，是研究其他网络的基础，常作为学习神经网络的起点。单层感知器是一个具有一层神经元、采用阈值激活函数的前向网络，模型结构如图9.4.5所示。

图9.4.5 感知器结构示意图

M类问题的判别规则，也即神经元的输出函数定义为

由式（9.17）、式（9.18）可知，由网络要进行正确的判决，关键在于输出层中的每一个神经元必须有一组合适的权值。感知器采用监督学习算法得到权值，从而建立模式判别的能力。当依次输入学习样本时，用期望输出与实际输出之差来修正网络的连接权，权值的更新采用最简单的学习规则，通过迭代算法最终得到希望的权值。

算法描述如下：

第一步：设置初始权值wij (1)。通常各权值的初始值设置为较小的非零随机数，w(n+1)j为j个神经元的阈值。

第二步：输入新的模式向量。

第三步：计算神经元的实际输出。设第k次输入向量为Xk，与第j个神经元相连的权向量为Wj=(w1 j,w2j,…,wn j,w(n+1)j )T ，则第j个神经元的实际输出为

第四步：修正权值。设dj为第j个神经元的期望输出，则权值按下式修正为

第五步：转到第二步。

当全部学习样本都能利用某一次迭代得到的权值正确分类时，学习过程结束。可以证明，当模式类线性可分时，上述算法在有限次迭代后收敛。

迭代过程中，权向量的修正量与输入模式Xk成正比，比例因子为δ[d j-y j(k )]。若δ取值太大，算法可能出现振荡；δ取值太小，收敛速度会很慢。经验证明，当δ随k的增加而减少时，算法一定收敛。

2. BP神经网络

BP（Back Propagation）神经网络于1986年由Rumelhart和McCelland为首的科学家小组提出，是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP网络能学习和存储大量的输入—输出模式映射，而无须事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。

BP神经网络模型由输入层、中间层和输出层组成，中间层可扩展为多层。一般的多层前向神经网络结构如图9.4.6所示，相邻层之间各神经元进行全连接，即左层的每一个神经元与右层的每一个神经元都有连接，而各层神经元之间无连接。BP神经网络按有监督学习方式进行训练，当一对学习模式提供给网络后，其神经元的激活值将从输入层经各隐含层向输出层传播，在输出层的各神经元输出对应于输入模式的网络响应。然后，按减少希望输出与实际输出误差的原则，从输出层经各隐含层，最后回到输入层逐层修正各连接权。此过程反复交替进行，直至网络的全局误差趋于给定的极小值，即完成学习的过程。由于这种修正过程是从输出到输入层逐层进行的，所以称它为“误差逆传播算法”。随着这种误差逆传播训练的不断修正，网络对输入模式响应的正确率也将不断提高。

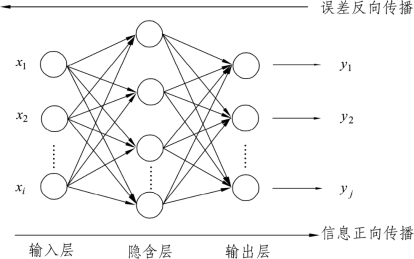
图9.4.6　三层BP网络模型结构

现介绍采用S型函数的多层前向神经网络的学习方法，即网络的激活函数采用S型函数：(www.xing528.com)

这是因为S型函数具有很好的函数特性，其效果又近似于符号函数。

假设有一个K层的神经网络，从第0层到第1层的原始输入量、权矩阵、第一层神经元接受向量和第一层输出向量以及它们之间的关系分别为

第k-1层到第k层的权矩阵、神经元接受向量和输出向量以及它们之间的关系分别为

θj为神经元的阈值；

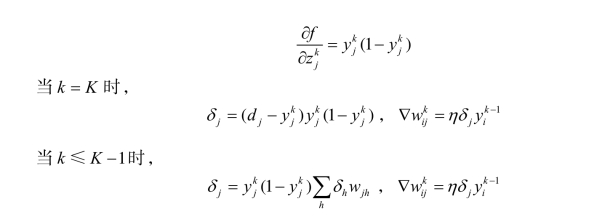
采用S型函数的多层前向神经网络的BP算法具体步骤如下：

第一步：对权值和神经元阈值初始化。给所有权值和阈值赋(0, 1)上分布的随机数。

第二步：输入样本指定输出层各神经元的希望输出值d1 ,d2,…,dnK 。

第三步：依次计算每层神经元的实际输出，直到计算出输出层各神经元的实际输出。

第四步：修正每个权值。从输出层开始，逐层向低层递推，直到第一隐层。修正公式为

如果神经元j是输出层的一个神经元（即k=K），则

如果神经元j是隐层的一个神经元（即k≤K-1），则

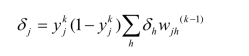
第五步：计算误差函数。若为单样本神经网络，其误差函数为

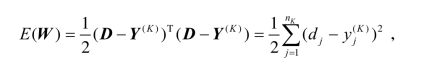
若有N个样本，其误差函数为

第六步：判断网络误差是否满足要求。当误差达到预设精度或学习次数大于设定的最大次数，结束算法；否则，选取下一个学习样本及对应的期望输出，返回到第三步，进入下一轮学习。