实用数学方法：灰色关联度分析

灰色系统理论提出的灰色关联分析是在不完全的信息中，对所要分析研究的各种要素，通过一定的数据处理，在随机的因素序列间，找出它们的关联性，发现主要矛盾，抓住影响系统的主要特征以及主要因素。它根据因素之间发展态势的相似或相异程度，亦即“灰色关联度”，来衡量因素间接近的程度。关联分析是按发展态势做分析，因而对样本量的大小没有太高的要求，分析时也不需要典型的分布规律，而且分析的结果一般与定性分析相吻合，所以具有广泛的实用性。

灰色关联分析是基于行为因子序列的微观或宏观几何接近，以分析和确定因子间的影响程度或因子对主行为的贡献测度而进行的一种分析方法。其基本思想是根据序列曲线几何形状的相似程度来判断其关系是否紧密，曲线越接近，变化趋势也越接近，相应序列之间的关联度越大，反之则越小。

灰色关联度分析的步骤有：

（1）确定比较数列和参考数列，进行数据处理。

（2）计算灰色关联系数。

（3）计算灰色关联度。

（4）关联度按大小排序，评价分析。关联度越大，其评价结果越好。

1. 数据列的处理

对一个抽象的系统或现象进行分析，首先要选准反映系统行为特征的数据序列，即找到系统行为的映射量，用映射量来间接地表征系统行为。如用国民平均接受教育的年数来反映教育发达程度，用刑事案件的发案率来反映社会秩序和社会治安情况，用医院挂号次数来反映国民的健康水平等。有了系统行为特征的数据和相关因素的数据，即可相应地绘制与各个序列对应的折线图，从直观上进行分析。如果系统行为特征映射量和各个相关因素的意义、量纲完全相同，可以直接对它们之间的关系进行分析。当系统行为特征映射量和各个相关因素的意义、量纲不同时，则需要对系统行为特征映射量和各个相关因素进行适当处理，使之化为数量级大体相近的无量纲数据，并将负相关因素转化为正相关因素。

定义1 设xi为系统因素，其在序号k上的观测数据为xi (k ),k=1,2…,n，则称

为因素xi的行为序列。若k为时间序号，xi (k)为因素xi在k时刻的观测数据，则称为因素xi的行为时间序列；若k为指标序号，xi (k)为因素xi关于第k个指标的观测数据，则称为因素xi的行为指标序列；若k为观测对象序号，xi (k)为因素xi关于第k个对象的观测数据，则称为因素xi的行为横向序列。

无论是时间序列数据、指标序列数据还是横向序列数据，都可以用来作关联分析。

设行为序列为xi=（(xi(1),xi(2)),…,xi (n)），i=1,2,…,m常用的处理方法有初值法、均值化、区间值化。

（1）初值化。

（2）均值化。

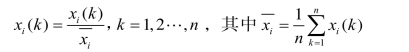
（3）区间值化。

一般地，数据的初值化、均值化、区间值化不宜混合、重叠作用，在进行系统因素分析时，可根据实际情况选用其中的一个。

若系统因素ix与系统主行为呈负相关关系，我们可以将其逆化或倒数化后进行计算。

（4）逆化。

（5）倒数化。

若为非时间序列，数列中不同指标的数在大小上相差较大，在同一指标下可人为设定一个数处理，使同一指标下的数量级相同，这种方法称为规一化。

例如，设

因此对赫兹、秒、链、毫秒、转/分钟，分别可用10000赫兹、10秒、10链、10毫秒、100转/分钟作单位，则得到生成数列

2. 灰关联系数的计算

定义2 设参考数列为

(www.xing528.com)

比较数列为

则定义x0(k)与xi (k)的关联系数为

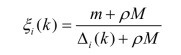
其中：ρ∈(0,+∞)称为分辨系数。ρ越小，分辨力越大。一般ρ的取值区间为[0, 1]，更一般地，取ρ=0.5，ρ的取值可视具体情况而定。

3. 关联度的计算

从关联系数的计算来看，我们得到的是各比较数列与参考数列在各点的关联系数值，结果较多，信息过于分散，不便于比较，因此有必要将每一比较数列各个时刻（或指标、对象）的关联系数集中体现在一个值上，这一数值即是关联度。

定义3 设参考数列为

比较数列为

则关联度定义为

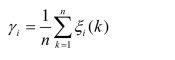
关联度的常见性质有：

在计算加权关联度时，合理地确定权数这一重要影响因素。常用的权数确定方法包括专家估测法、频数统计分析法、主成分分析法、模糊逆方程法以及层析分析法等。

4. 灰色关联度分析实例

例1（供应商选择决策） 某核心企业需要在6个待选的零部件供应商中选择一个合作伙伴，各待选供应商有关数据见表9.1.2。

表9.1.2　某核心企业待选供应商的指标评价有关数据

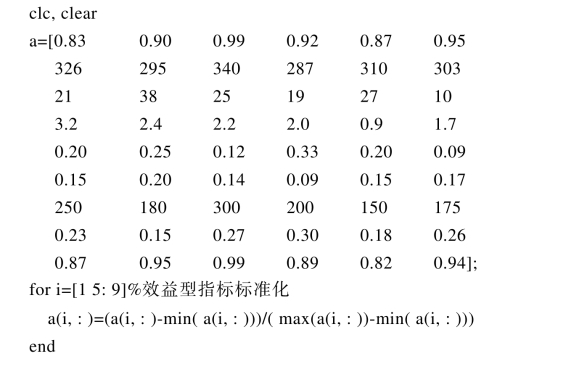
产品质量、技术水平、经济效益、供应能力、市场影响度、交货情况指标属于效益型指标；产品价格、地理位置、售后服务指标属于成本型指标。现分别对上述指标进行规范化处理，规范化数据结构见表9.1.3。取各指标值的最大值，得到虚拟最优供应商。

表9.1.3　比较数列和参考数列值

取ρ=0.5，计算ξi (k)及ri，具体数值见表9.1.4。

表9.1.4　关联系数和关联度值

由表9.1.4，按灰色关联度排序，r4 ＞r3 ＞r6 ＞r2 ＞r5 ＞r1，由于供应商4与虚拟最优供货商的关联度最大，即供应商4优于其他供应商，企业决策者可以优先考虑从供应商4处采购零部件以达到整体优化。

将灰色关联分析用于供应商选择决策中，可以针对大量不确定性因素及其相互关系，将定量与定性方法有机结合起来，使原本复杂的决策问题变得清晰简单，且计算方便，并可在一定程度上排除决策者的主观任意性，得出的结论也比较客观，有一定的参考价值。

MATLAB程序如下：