例1 生育率受社会、经济、文化、计划生育政策等很多因素影响,但这些因素对生育率的影响并不是完全独立的,而是交织在一起,如果直接用选定的变量对生育率进行多元回归分析,最终结果往往只能保留两三个变量,其他变量的信息就损失了。因此,考虑用因子分析的方法,找出变量间的数据结构,在信息损失最少的情况下用新生成的因子对生育率进行分析。
选择的变量有:多子率、综合节育率、初中以上文化程度比例、城镇人口比例、人均国民收入。表8.4.1是1990年中国30个省、自治区、直辖市的数据,详细数据见本章附表1。
表8.4.1 生育率有关数据
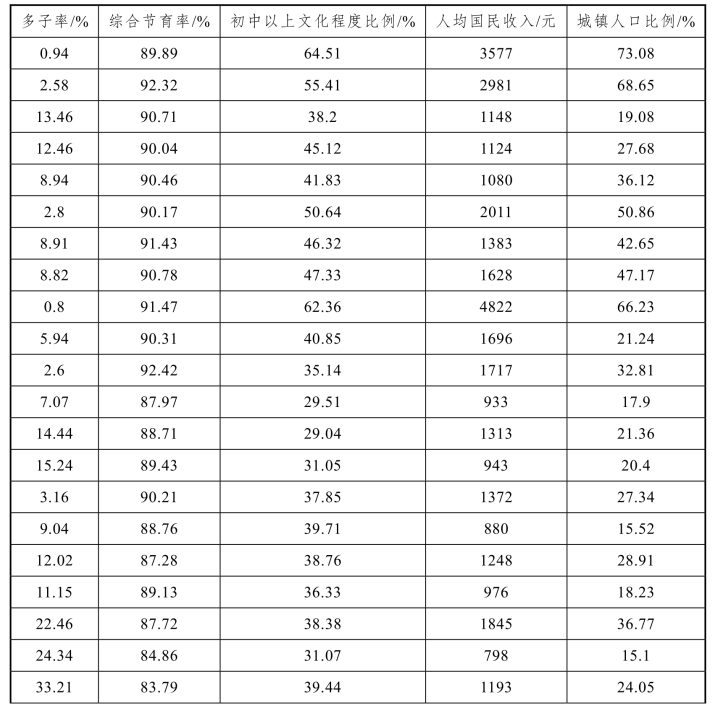
续表
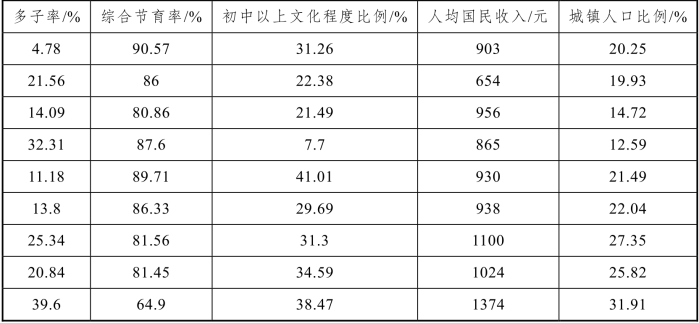
通过因子分析,本例中我们得到了两个因子:第一个因子是社会经济发展水平因子,第二个因子是计划生育因子。有了因子得分值后,则可以利用因子得分进行其他的统计分析。
MATLAB程序如下:

表8.4.2 解释的总方差
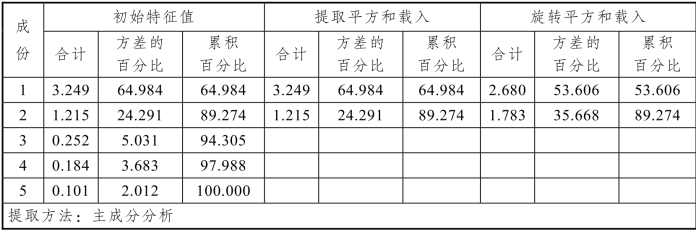
表8.4.3 成分矩阵
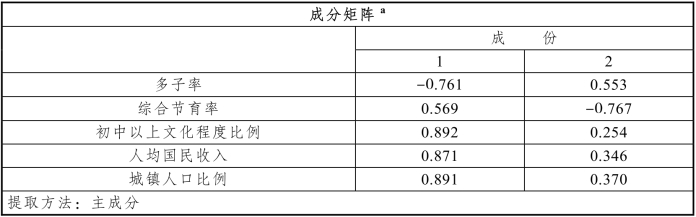
注:a. 已提取了2个成分。
下面在SPSS中对例1数据进行因子分析。
由图8.3.2进入因子分析SPSS操作,单击图8.3.3的旋转按钮,弹出图8.3.4,选择旋转方法:主成分分析就选默认的“无”,如果是因子分析根据实际情况选择,这里选择“最大方差法”(Varimax)……完成所有设置后,单击“OK”按钮,便可输出系列结果。
表8.4.4 旋转成分矩阵
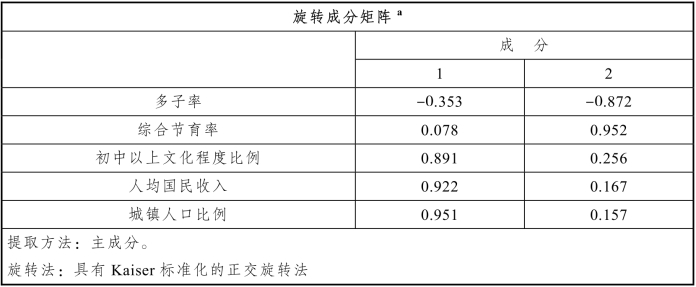
注:a. 旋转在3次迭代后收敛。
当我们用x1, x2, x3, x4, x5表示变量多子率、综合节育率、初中以上文化程度比例、人均国民收入、城镇人口比例,确定两个因子f1和f2,SPSS输出旋转成分矩阵见表8.4.4,用因子f1和f2来表示与原来变量的关系:
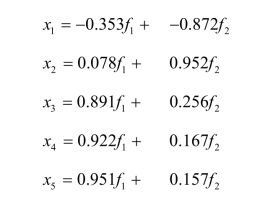
这里,第一个因子f1主要和初中以上文化程度比例、人均国民收入、城镇人口比例有很强的正相关,相关系数绝对值都比较大,分别为0.891,0.922,0.951;第二个因子f2主要和多子率、综合节育率有很强的相关性,相关系数分别为-0.872,0.952。因此,第一个因子命名为“社会经济发展水平因子”,第二个因子命名为“计划生育因子”。由此看出,通过旋转,因子分析的结果的解释性比主成分分析更强,把不同性质的变量区分得更清楚。这里的系数所形成的载荷图(见图8.4.1)直观地反映了这个特点。
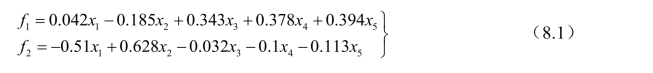
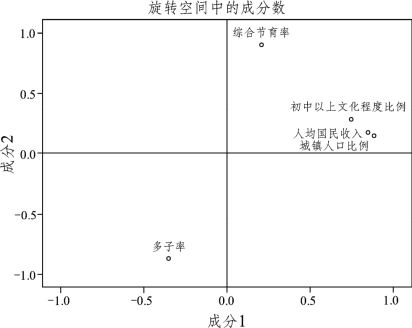
图8.4.1 因子载荷图:原始变量和两个因子的线性相关关系
表8.4.5 成分得分系数矩阵
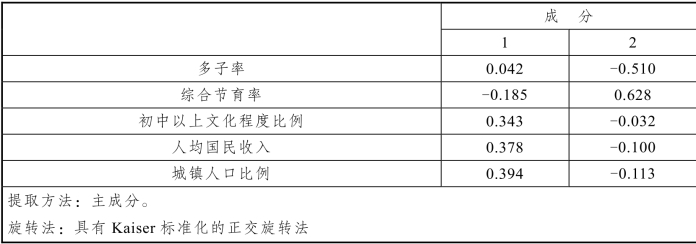
表8.4.5给出了因子f1和 f2如何用原来变量来表示,第一和第二主因子(习惯上用字母f来表示因子)可以按照如式(8.1)计算因子得分:计算出每个地区的第一个因子和第二个因子的因子得分f1和f2的大小,这里x1, x2, x3, x4, x5是各变量标准化后的值,如依次代入第一行各变量的标准化以后的值:-1.244 67, 0.438 45,2.304 59, 2.381 16, 2.634 6,即得第一行的FAC1_1=2.595 32,FAC2_1=0.299 25,从而对每个地区分别按照这两个因子排序。
需要注意的是,因子分析可以看成主成分分析的推广,它也是多元统计分析中常用的一种降维方式,因子分析所涉及的计算与主成分分析很类似,在SPSS中,它们属于同一个总选项,操作界面相同,只是选项有所不同。主成分分析是因子分析的一种方法,也可以说,主成分分析仅仅是因子分析的一个特例。它们的主要目的都是用少数几个互相正交的新变量(因子分析也可以选择不正交的因子)来作为原始变量的代表,这些新变量叫作因子或者成分。但差别也是很明显的:
(1)主成分分析把方差划分为不同的正交成分,而因子分析则把方差划归为不同的起因因子。
(2)主成分分析仅仅是变量变换,而因子分析需要构造因子模型。
(3)主成分分析中原始变量的线性组合表示新的综合变量,即主成分;因子分析中潜在的假想变量和随机影响变量的线性组合表示原始变量。
主成分分析的数学模型本质上是一种线性变换,是将原始坐标变换到变异程度大的方向上,相当于从空间上转换观看数据的角度,突出数据变异方向,归纳重要信息;而因子分析从本质上看是从可测变量去“提炼”潜在因子的过程。因此,虽然因子分析和主成分分析的目的一致,但因子分析更精密、结果更有解释性。
因子分析和主成分分析都依赖于原始变量,也只能反映原始变量的信息,所以原始变量的选择很重要,一定要符合进行分析所要达到的要求:数据越相关,降维效果就越好。
在用因子得分进行排序时要特别小心,由于原始变量不同,因子的选取不同,排序可能不一样,特别是对于敏感问题。
因子分析与回归分析不同,因子分析中的因子是一个比较抽象的概念,而回归变量有非常明确的实际意义。因子分析有确定的模型,观察数据在模型中被分解为公共因子、特殊因子和误差三部分。
习 题
1. 讨论判别分析和聚类分析有什么不同。
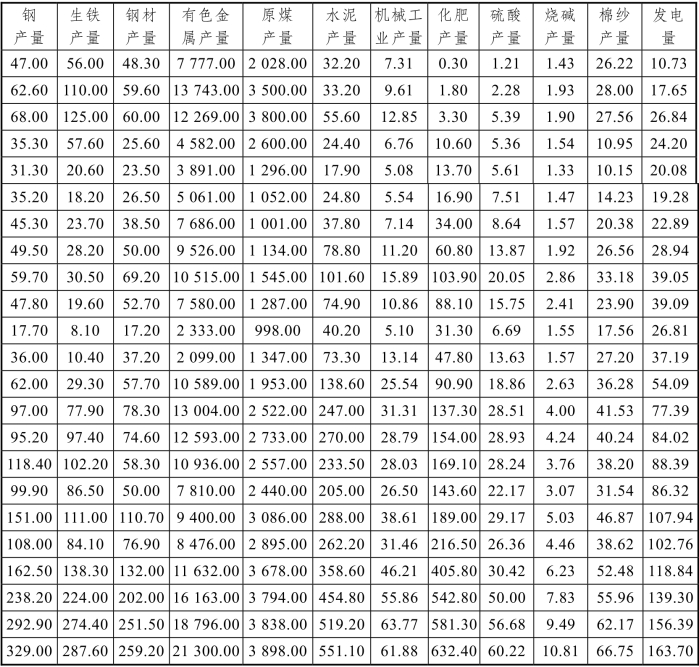
2. 假定影响某地区发电需求量的指标有:钢产量、生铁产量、钢材产量、有色金属产量、原煤产量、水泥产量、机械工业产量、化肥产量、硫酸产量、烧碱产量、棉纱产量,共11个指标,收集了1958—1980年共23年的各指标和观测值发电量(见表1),构造电量需求模型。
(1)对数据标准化;
(2)分别对原始数据和原始数据标准化后的数据进行主成分分析并比较;(https://www.xing528.com)
(3)求发电量关于钢产量、生铁产量、钢材产量、有色金属产量、原煤产量、水泥产量、机械工业产量、化肥产量、硫酸产量、烧碱产量、棉纱产量的回归方程,并与上述计算结果进行比较。
表1
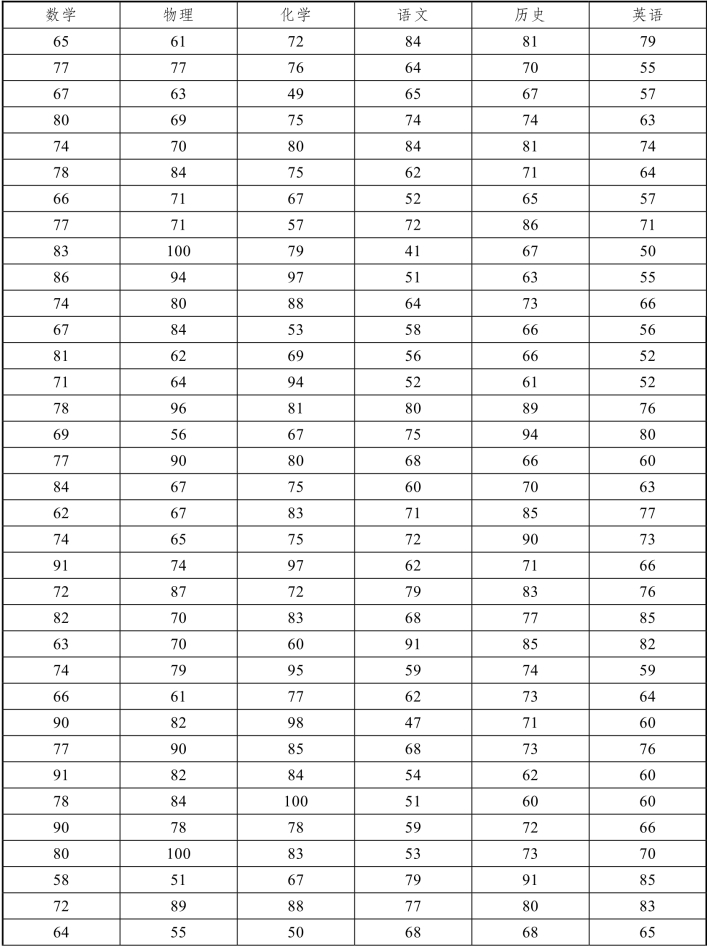
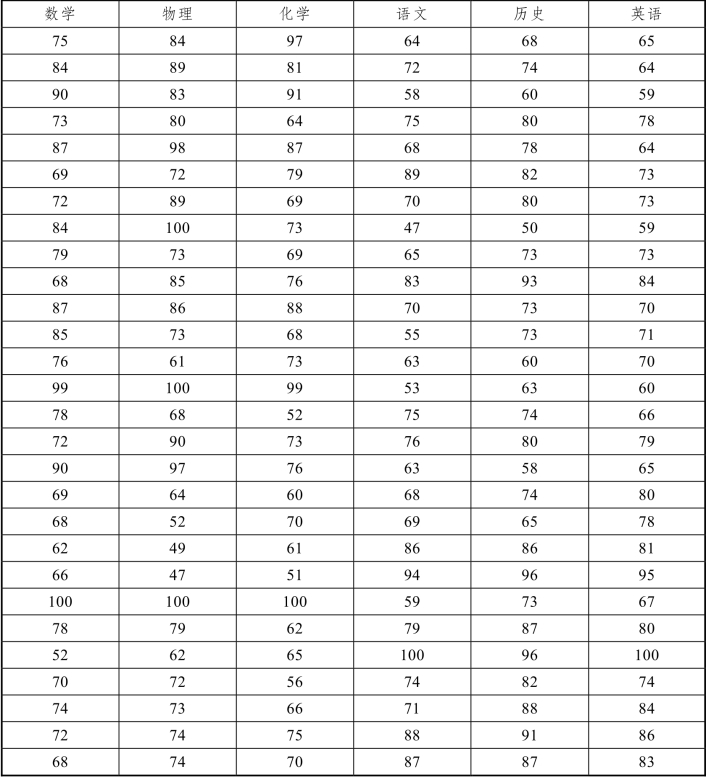
3. 针对不同选项,对100名学生的成绩进行主成分分析和因子分析(数据见表2)。
表2
续表
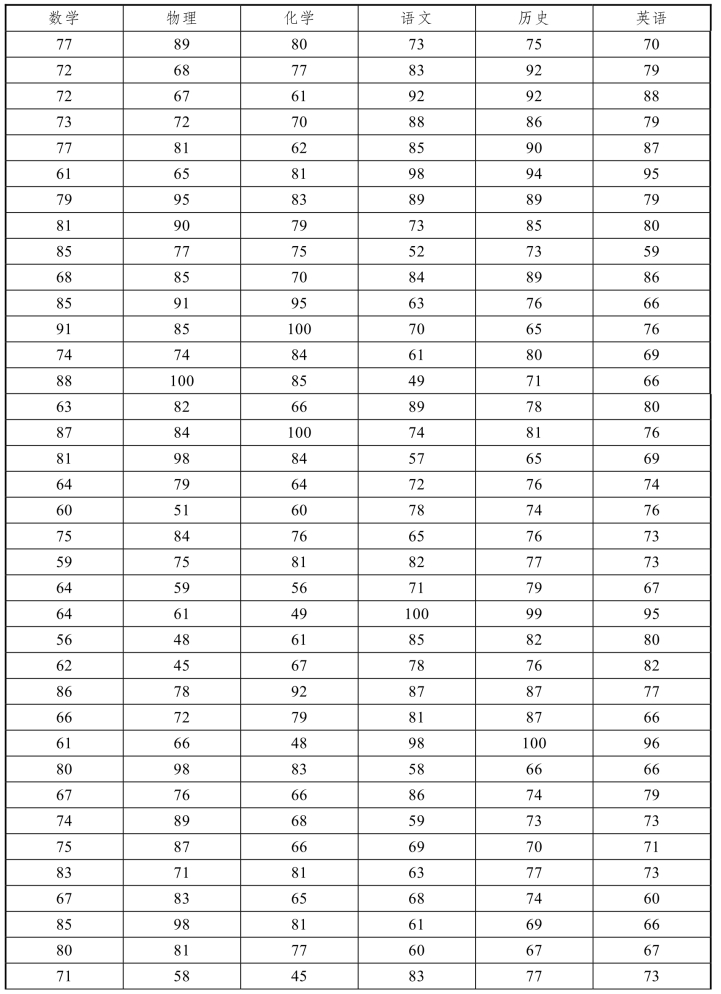
续表
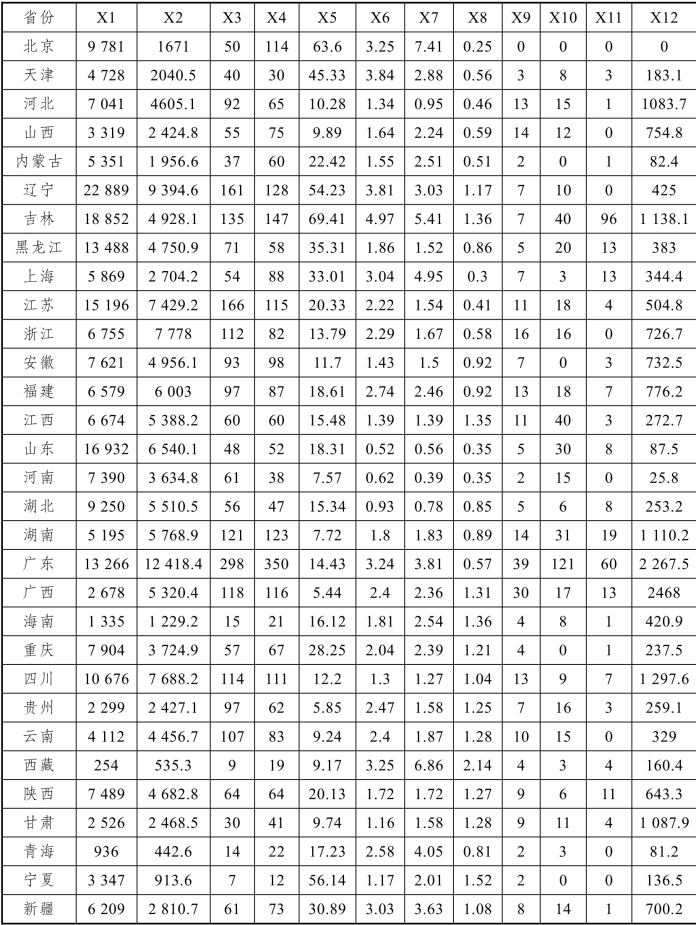
4. 对表3中数据进行主成分分析。
火灾基本指标:X1,火灾起数(单位:起);X2,火灾经济损失(单位:万元);X3,火灾死人(单位:人);X4,火灾伤人(单位:人)。
火灾经济指标:X5火灾发生率(单位:起/十万人口);X6火灾死亡率(单位:人/百万人口);X7,火灾伤人率(单位:人/百万人口);X8,火灾损失率(单位:元/万元GDP)。
重特大火灾指标:X9,重特大火灾起数(单位:起);X10,重特大火灾死人(单位:人);X11,重特大火灾伤人(单位:人);X12,重特大火灾经济损失(单位:万元)。
表3
5. 对8.3节中例1数据,只选取少数两三个变量进行计算,观察结果有什么不同。尝试在SPSS上选择各种不同的选项,然后比较结果,并分析原因。
附录1
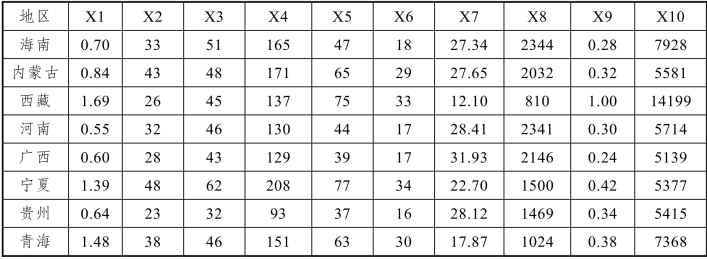
X1为每百万人口高等院校数;
X2为每十万人口高等院校毕业生数;
X3为每十万人口高等院校招生数;
X4为每十万人口高等院校在校生数;
X5为每十万人口高等院校教职工数;
X6为每十万人口高等院校专职教师数;
X7为高级职称占专职教师的比例;
X8为平均每所高等院校的在校生数;
X9为国家财政预算内普通高教经费占国内生产总值的比重;
X10为生均教育经费。
附表1
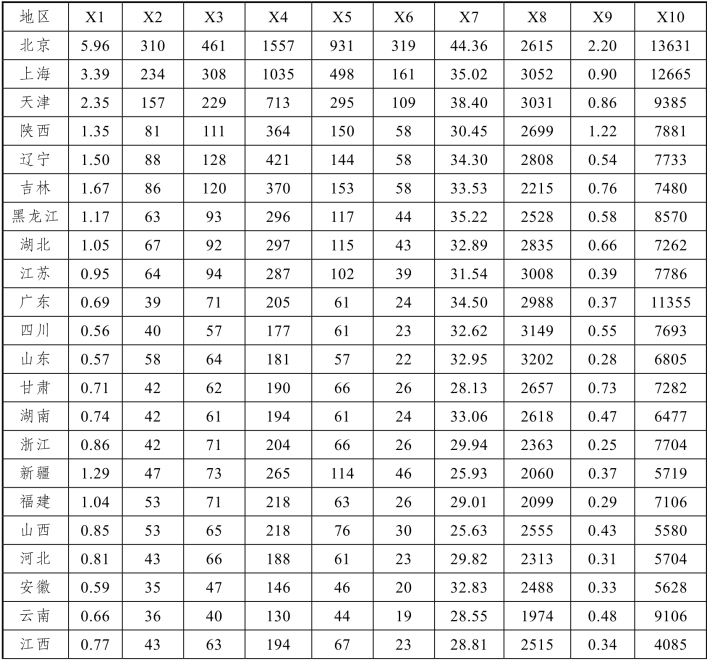
续表
附录2
附表2
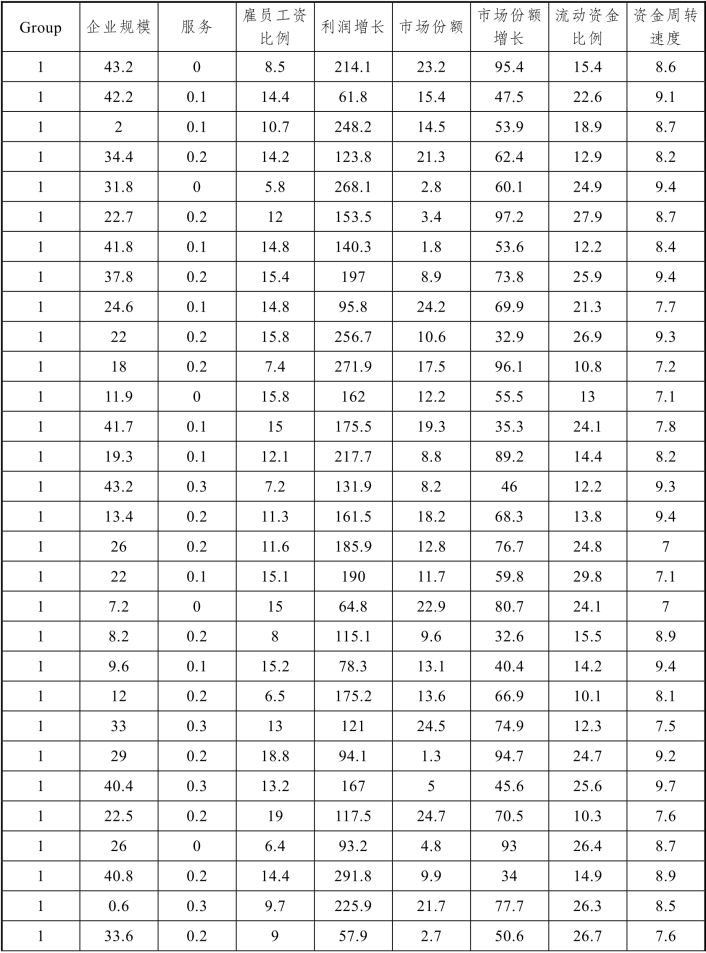
续表
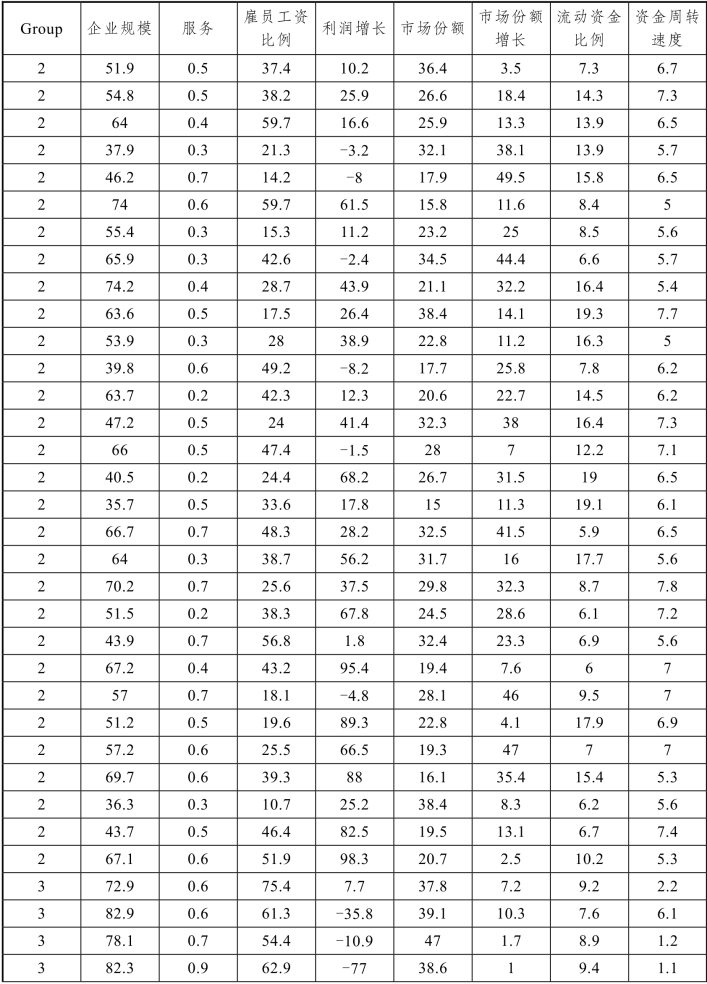
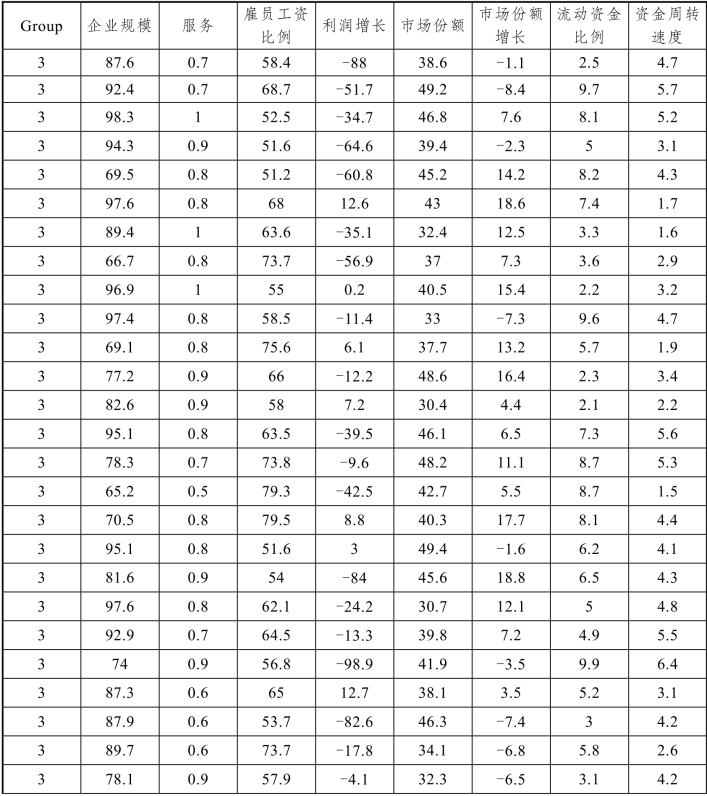
续表
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




