实用数学方法：主成分降维技术的应用

设对某一事物的研究涉及n个相关变量，分别用X 1,X2,…,Xn表示，这n个变量构成的n维随机向量为X=(X 1,X2,…,Xn)T。做如下线性变换：

这个线性变换需要满足 (i ,j=1,2,…,n)：

（1）每个Yi的系数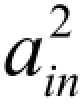： ++...+=1（限定在单位圆上的特征向量，它代表一个“方向”，即常说的主成分方向，不然方差可以任意增大而没有意义，因为任意非零数乘以特征向量仍是特征向量）。

（2）Y1 ,Y2,…,Yn尽可能不含重复信息，线性无关，即Cov(Yi ,Yj)=0，i≠j。

（3）Y1是一切满足第（1）条的线性组合中方差最大者；(www.xing528.com)

Y2与Y1线性无关，是一切满足第（1）条的线性组合中方差最大者，也即在所有方差中，第二大；……；

Yk与Y1 ,Y2,…,Yk-1线性无关，是一切满足第（1）条的线性组合中方差最大者，也即在所有方差中，第k大。

具体选取几个主成分，要依实际情况而定。用k(k≤n)个新变量来代替n个原始变量，达到了降维的目的，而且损失的信息并不多。我们把这种做法称为主成分降维技术。如果所涉及的变量都不怎么相关，就很难降维了。

主成分分析的结果受量纲的影响，由于各变量的单位可能不一样，如果各自改变量纲，结果会不一样，所以实际中可以先把各变量的数据标准化，然后使用协方差矩阵或相关系数矩阵进行分析。在SPSS中，无须标准化，因为SPSS就是后台对原始数据标准化以后再进行分析的。