天水GDP数据分析结果

地区生产总值（GDP）反映该地区总的经济状况，是政府制定相关政策的重要依据，也常作为预测模型的重要变量。例如，天水市属暖温带半湿润半干旱气候，夏天凉爽，而冬天气候适宜，一般年降水量570毫米左右，森林覆盖率36.45%，非常适合人类居住，号称“陇上小江南”。选取1980—2010年天水地区GDP数据（见表7.5.2），并通过时间序列模型对未来3年的数据进行预测。

表7.5.2　甘肃天水GDP　　　　　　　　　单位：万元

1. 利用ARIMA模型对未来三年GDP进行预测

（1）绘制时序图。

由于直接采用年份作为时间变量，取值较大，故时间变量t={1,…,31}，时序图如图7.5.1所示。

图7.5.1　天水GDP时序图

根据时序图可知，天水GDP时间序列不平稳，大致呈现二次曲线形状，且没有周期趋势，初步判定2阶差分即可提取确定性信息，转化为平稳时间序列。

（2）对2阶差分序列进行探索分析。

打开SPSS后，单击“分析”→“时间序列预测”→“自相关性”，将“GDP”移入变量文本框，模型选中“差异”文本框，填入差分次数“2”，单击“确定”，如图7.5.2所示，部分运行结果如下。

图7.5.2　自相关性对话框

显然，天水GDP二阶差分序列呈现平稳性质。另外，由表7.5.3可知，GDP二次差分序列短期具有相关性，延迟6阶的P值仅为0.028，故拒绝原假设，即它不是白噪声，具有进一步分析的价值，初步判定可建立ARMA模型。下面利用自相关图和偏自相关图（见图7.5.4、图7.5.5）进行模型定阶。

图7.5.3　天水GDP二阶差分序列时序图

表7.5.3　天水GDP二阶差分序列的白噪声检验

注：a. 假定的基本过程为独立性（白噪声）；b. 基于渐近卡方近似值。

图7.5.4　天水GDP二阶差分后自相关图

图7.5.5　天水GDP二阶差分后偏自相关图

由偏自相关图可知，样本偏相关系数1阶截尾，可建立AR(1)模型。实际上，根据自相关图，读者也可尝试建立MA(1)、ARMA(1,1)模型。考虑到模型的可解释性，本文选择AR(1)模型。

（3）建立ARIMA(1,2,0)模型。

单击“分析”→“时间序列预测”→“创建传统模型”，打开时间序列建模器对话框并做相应设置，单击“确定”，如图7.5.6所示，部分运行结果如下。

平稳R2统计量取负值时，表示当前模型没有基本均值模型好；取正值时，表示当前模型优于基本均值模型。R2用来估计模型解释的变异在总变异中的比例，由表7.5.4可知，本例中R2为0.997，效果很好。模型显著性检验转化为残差序列的白噪声序列检验，P值为0.800，即残差序列为白噪声序列，模型有效。另外，由残差序列的自相关图与偏自相关图（见图7.5.7），也可认为残差序列为白噪声序列。

表7.5.4　模型统计

图7.5.6　时间序列建模器对话框

表7.5.5　ARIMA模型参数

由表7.5.5可知，参数的显著性检验的P值小于0.05，参数显著性检验通过。总之，本模型显著性检验通过，参数显著性检验通过，且R2很高，可用于预测，三期预测结果见表7.5.6。

图7.5.7　残差序列的自相关图与偏自相关图

表7.5.6　三期预测

2. 利用自回归模型对未来三年GDP进行预测

将历史观察值{xt-1,…,xt -k }作为自变量，建立多元线性回归模型，即(www.xing528.com)

假定k=3，即利用过去三年的观测值预测未来，多元线性回归模型的SPSS实现如图7.5.8所示，参数设置同线性回归，部分运行结果见表7.5.7。

图7.5.8　线性回归对话框

表7.5.7　延迟三期自回归模型的参数估计

注：a. 因变量：GDP。

显然，延迟2期、3期及常数项的参数估计不显著，可删去重新做线性回归，部分运行结果见表7.5.8和7.5.9。注意，在“线性回归：选项”对话框中可删去常数项。

表7.5.8　延迟1期自回归模型的模型摘要

注：a. 预测变量：GDP1。
b. 对于过原点回归（无截距模型），R2用于衡量因变量相对于此回归所解释的原点的可变比例。此R2不能与针对包含截距的模型的R2进行比较。
c. 因变量：GDP。
d. 过原点线性回归。

表7.5.9　延迟1期自回归模型的参数估计

注：a. 因变量：GDP；b. 过原点线性回归。

由表7.5.8可知，线性回归模型的调整后R2为0.999，非常高，模型显著性检验的P值远小于0.05，即模型显著，可用于预测。由表7.5.9可知，建立的自回归模型为

未来的三期预测值分别为3 437 616万元、3 936 071万元、4 506 801万元。

真实数据很难完全满足模型假设，故模型运行结果很难像理论那样完美，这需要建模者具备一定的自我判断能力，不能太死板、拘泥细节，要抓住主要目标。ARIMA模型需要假定外界环境大致不变，且数据不具有异方差现象，而在现实中，这两个条件都很难满足。由GDP二阶差分序列时序图可知，本例具有一定的异方差性，并不完全符合ARIMA模型的假设，但是，从建立的ARIMA(1,2,0)模型来看，整体效果还是很好，可以满足一般的预测需求，未来三期的预测值分别为3 409 315万元、3 860 986万元、4 334 506万元。那么，真实情况如何呢？甘肃省统计局公布的（2011年至2013年）天水市GDP依次为357.60亿元、412.87亿元、454.34亿元，预测值略低于真实值，具有参考价值。这主要是因为甘肃天水的外界条件发生了一定变化，相对而言，经济发展更好了。利用自回归模型得到未来三期的预测值分别为3 437 616万元、3 936 071万元、4 506 801万元，预测效果更好，即简单模型的预测效果超过了复杂的预测模型。（其实，研究未来是最难的，尤其是社会科学。）

习 题

1. 表1是1986—2007年的统计数据，请根据这些数据研究全国口岸交通运输工具出入境总数的变化规律。

表1　1986—2007年出入境交通工具统计数据

2. 7.2节中给出了两种S形生长曲线，对称型的Logistic曲线的表达式为

非对称型的Gompertz曲线的表达式为

当上述两个表达式中的“K”都未知时，试对它们分别进行适当的变换，使之都转化为修正指数模型（提示：转换后的修正指数模型对应图7.2.7单调递减的情形）。

3. 表2给出了某市1976—1987年某种电器的销售额，试预测1988年该电器的销售额。

表2　1976—1987年某种电器的销售额

4. 根据表3提供的1994—2004年内地居民赴港澳地区审批情况的统计数据进行数据分析。

表3　1994—2004年内地居民赴港澳地区审批情况的统计数据

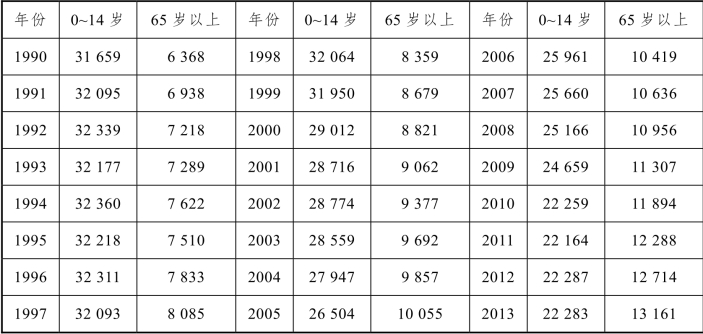
5. 表4给出了1990—2013年我国按年龄分组的0～14岁儿童和65岁以上老人的人口数（单位：万人），试对其分析并对未来几年做出预测，并比较与真实值的差异（数据来自国家统计局）。

表4　1990—2013年我国0～14岁儿童和65岁以上老人的人口数

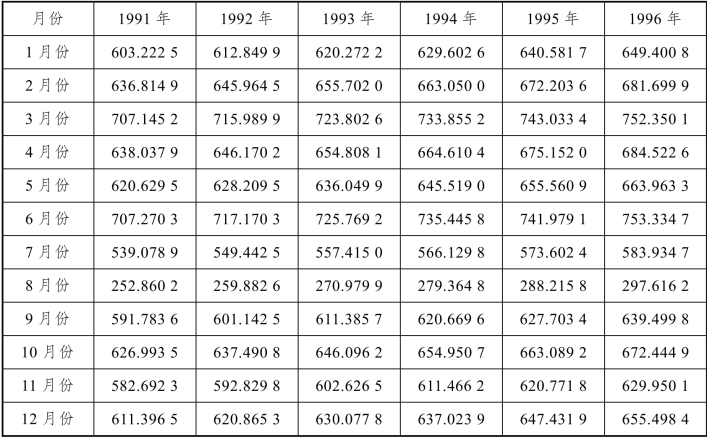
6. 表5给出了某商品1991—1996年的月销售额（单位：万元），试对数据进行分析并预测未来一年的销售额。

表5　某商品1991—1996年的月销售额