平稳时间序列建模-实用数学方法

运用ARMA模型的前提是，时间序列为平稳时间序列。对于包含趋势性或季节性的非平稳时间序列，不能直接用ARMA模型去描述，须经过适当的逐期差分或季节差分消除其趋势影响后，再对形成的新的平稳序列建立ARMA(p,q)模型进行分析。

假定某时间序列经过预处理，可以判定为平稳非白噪声序列，我们可以对该序列进行建模。

（1）计算时间序列的样本自相关系数和样本偏自相关系数。

（2）根据样本自相关系数和样本偏自相关系数的性质对模型进行定阶。

（3）估计模型中的未知参数。

（4）检验模型的有效性。如果拟合模型没有通过检验，转向步骤（2），重新选择模型拟合。

（5）模型优化。如果拟合模型通过检验，仍转向步骤（2），考虑多种可能性，建立多个拟合模型。从通过检验的拟合模型中选择最优模型。

（6）根据拟合模型，预测序列的将来走势。

建立ARMA模型的关键在于定阶，即确定参数p,q，余下工作可交给统计软件自动实现。ARMA(p,q)模型定阶的基本原则见表7.5.1。

表7.5.1　ARMA(p,q)模型定阶的基本原则

但在实践操作中，这个定阶原则存在困难，因为由于样本的随机性，本应截尾的样本自相关系数和偏自相关系数会呈现小值振荡。同时由于平稳序列通常具有短期相关性，随着延迟阶数k→∞，ˆkρ和ˆkkφ会衰减到0并呈现小值振荡，所以我们实际上没有绝对的标准，在很大程度上需依靠分析员的主观判断。但样本自相关系数和偏自相关系数的近似分布可以帮助经验缺乏的分析人员做出尽可能合理的判断。

所以可用2倍标准差辅助判断。

当和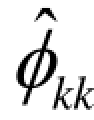在最初的d阶明显大于2倍标准差，而后几乎95%的自相关系数都落在2倍标准差内，且由非零衰减到小值的速度非常快，这时可认为自相关系数d阶截尾。如果有超过5%的样本相关系数落入2倍标准差范围之外，或者是由明显非零的相关系数衰减为小值波动的过程比较缓慢或者非常连续，这时通常视为相关系数不截尾。

一般，似然函数值越大说明模型拟合效果越好，模型中未知参数个数越多，拟合的准确度会越高，但未知的风险也越多，参数估计的难度越大，估计的精确度越差，因此最小信息量准则（An Information Criterion，简称AIC准则）是拟合精度和参数个数的加权函数：

对于一个观察值序列，序列越长，相关信息越分散，要使拟合精度比较高就需要多自变量的复杂模型。当样本容量很大时，在AIC准则中，拟合误差提供的信息受到样本容量的放大，但参数个数的惩罚因子却和样本容量无关，始终是2。为弥补不足，Schwartz在1978年提出SBC准则：(www.xing528.com)

理论上已证明：SBC准则是最优模型真实阶数的相合估计。在所有通过检验的模型中使得两准则最小的模型为相对最优模型。

由于对数似然函数

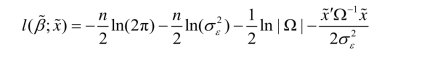
故在中心化ARMA(p,q)模型中，常采用

当一个拟合模型通过检验，说明在一定的置信水平下，该模型能有效观察序列的波动，但有效模型并不唯一，因此我们选择在所有通过检验的模型中使得AIC和SBC最小的模型为相对最优模型。

选择好拟合的模型后，下一步就是根据序列观测值估计模型的未知参数。利用数据得到拟合模型后，还要对拟合模型进行必要的检验。

1. 模型显著性检

模型是否显著有效主要看它提取的信息是否充分，一个好的拟合模型应该充分提取信息，残差序列将不再蕴含任何相关信息，即残差序列应该是白噪声，这样的模型称为显著性模型。所以，模型显著性检验就转化为检验残差序列的纯随机性检验。

2. 参数显著性检验

参数显著性检验即检验每个参数是否显著非零，它的目的是使得模型最精简。其实，参数不显著并不一定意味着拟合效果差，它只意味着那个自变量对因变量的影响不明显。如果把该自变量从模型中删除，最终模型将由一系列参数显著非零的自变量构成。在做参数估计检验时，如果某些参数通不过显著性检验且很难做剔除操作，可以不管，因为我们最关心的是整体，即模型显著性检验。

参数显著性检验的原假设和备择假设分别为

我们的最终目的是通过拟合模型对时间序列的发展趋势进行预测，即利用序列已观测到的样本值对未来某时刻的取值进行估计，目前对平稳序列最常用的预测是线性最小方差预测。线性是指预测值是观测值序列的线性函数，最小方差是预测方差最小。