三次指数平滑法-实用数学方法

前面提到，如果数据呈现直线趋势，那么需要对一次平滑结果进行直线修正；同理，如果数据大致呈曲线趋势，那么需要对一次平滑结果进行曲线修正。另外，前面提到的指数平滑法都是针对非季节性数据，若数据有季节性因素，怎么处理呢？

这些都需要用到三次指数平滑法。三次指平滑也称三重指数平滑，与二次指数平滑类似，它不直接将平滑值作为预测值，而是服务于模型建立。三次指数平滑法包括布朗三次指数平滑法及霍尔特-温特斯（Holt-Winter）季节性指数平滑法，前者主要用于非季节性且呈现二次曲线趋势的时间序列，后者分为加法和乘法两种模型，主要用于有趋势和季节性的时间序列。

1. 布朗三次指数平滑

常见的曲线修正是对时间序列呈现二次曲线趋势时进行修正，即当时间序列变化趋势为二次曲线趋势时，建立二次曲线模型对平滑结果进行修正，该方法就是布朗三次指数平滑法。其步骤为：先在二次平滑值基础上再进行一次指数平滑（三次平滑值），然后根据三次平滑结果建立二次曲线修正模型。

设时间序列为y1 ,y2,…,yt,…,yn，则三次平滑结果为

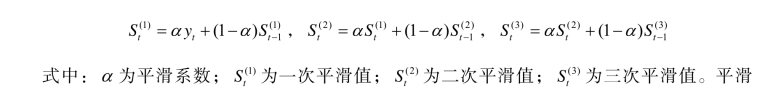
2. 霍尔特-温特斯（Holt-Winter）季节性指数平滑法

1）加法模型

该模型适用于具有趋势且季节效应随时间变化不大的序列，特别是有线性趋势和稳定的季节成分的序列，由三个平滑方程及一个预测方程构成：

最后的预测方程也可以写成

式中：yt为实际值；St为平滑项；tb为趋势项；tc为季节项；m为周期期数（月度数据取12，季度数据取4）；,αβ及γ为三个平滑系数；yˆt+l为第t+l时期的预测值。

2）乘法模型

该模型适用于具有趋势且季节效应随序列量级发生变化的序列，特别是有线性趋势和不稳定的季节成分的序列，同样由三个平滑方程及一个预测方程构成：

最后的预测方程也可以写成

加法模型中单个因子的效应被区分开来，它人为地忽略了相互作用；乘法模型则考虑了相互作用，随着数据的值增大，季节性的量也增长，大多数时间序列都呈现这种模式。当数据中季节性的量取决于数据值的时候，应该选择乘法模型；当季节性的量不取决于数据值的时候，应该选择加法模型，当然，如果不清楚的时候两种都应该尝试。

3）初始值的选取

3. 说明

布朗三次指数平滑法中的三个平滑方程都是从“水平层面”对平滑值进行的。而霍尔特-温特斯模型中的三个平滑方程除了水平层面外，还考虑了趋势与季节，霍尔特-温特斯模型可以看作布朗三次指数平滑法的变形。

运用SPSS操作时，不需要设置霍尔特-温特斯加法或乘法模型的三个平滑系数，系统会自动计算最优解。但SPSS没有提供布朗三次指数平滑法，计算时就需要至少选取两个平滑系数α，选择均方根误差较小者，该思路与7.3节运用趋势移动平均法计算例2类似。另外，对于含有季节性的时间序列，SPSS还给出了一种方法：简单季节性模型，该方法主要针对有季节性但无趋势的序列。

4. 实际应用

例2 表7.4.6给出了2013—2017年19个季度我国从空港出入境的人数（单位：人次），试对该数据进行分析并预测2019年第四季度我国从空港出入境人数。

表7.4.6　2013—2017年我国从空港出入境的人数(https://www.xing528.com)

（1）先绘制时间序列图，如图7.4.11所示。

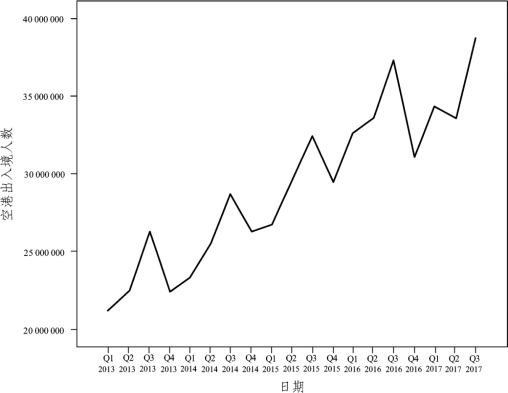
图7.4.11　空港出入境人数序列图

由序列图可知，该序列呈现出线性趋势并具有季节性，可以考虑用霍尔特-温特斯季节性指数平滑法进行分析预测。

（2）模型创建。SPSS操作时同样分为四步。

对于例2中的数据，完成前文的步骤①②后，在出现的对话框中（见图7.4.3）选择“季节性”中的“温特斯加性”或“温特斯乘性”，这里选择“温特斯乘性”。

步骤③与步骤④与例1都相同，注意“选项”中输入日期为“2019, 4”（见图7.4.12）。

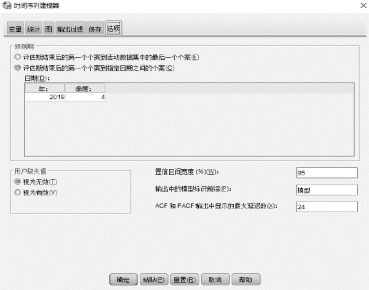
图7.4.12　时间序列建模器对话框

（3）模型结果。

模型统计（见表7.4.7）、指数平滑法模型参数（见表7.4.8）、残差图（见图7.4.13）及序列图（见图7.4.14），在SPSS的编辑页面会出现详细的预测值，部分截图见图7.4.15。

表7.4.7　模型统计

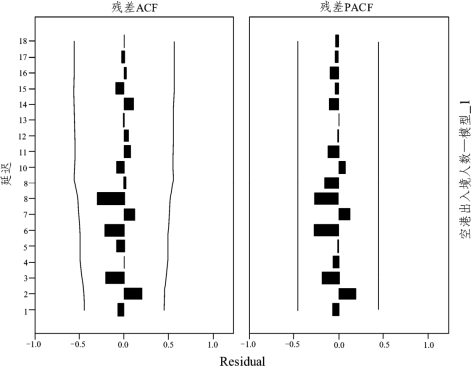
图7.4.13　残差序列的自相关图与偏自相关图

表7.4.8　指数平滑法模型参数

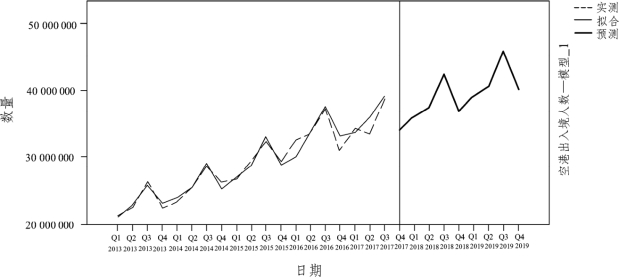
图7.4.14　预测值的序列图与实际值序列图

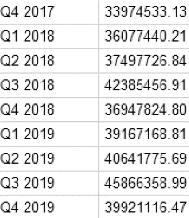
图7.4.15　预测值

（4）模型分析。

由表7.4.7可知，平稳R2为0.389，大于0，说明该模型优于简单均值模型，判别系数R2为0.957，即总变异中可以用温特斯乘法模型解释的部分占95.7%，且统计量杨-博克斯Q（18）对应的显著性水平为0.824＞0.05，说明模型拟合后的残差序列不存在自相关或偏自相关，这也反映在残差图（图7.4.13）中。整体来看，温特斯乘法模型拟合效果较好，这从预测值的序列图与实际值的序列图较贴合（图7.4.14）也能体现出来。

由表7.4.5可知，该模型在Alpha（水平）上差异有统计学意义（P值为0.058略大于0.05），其值为0.415，而参数Gamma（趋势）和Delta（季节）的统计学意义并不显著（均有P值＞0.1），尤其Gamma（趋势）不仅没有显著性（P值几乎为1）且值很小（0.001），说明本时间序列尽管为季节性数据，但其季节特征并不明显，且该序列的趋势特征更加不显著，即其所展现出来的趋势某种程度上用Alpha（水平）即可揭示。图7.4.15给出了从2017年第四季度至2019年第四季度的预测值。

另外，大家可以运用SPSS尝试其他方法，如温特斯加性等，根据R2最大、均方根误差（RMSE）和正态化（BIC）最小原则，查阅资料结合实际值比较后，选择拟合程度最优的模型进行预测，这里不再详述。