实用数学方法：二次指数平滑法

如果时间序列的变动出现直线趋势，那么运用简单指数平滑法会出现滞后偏差，就需要对一次平滑的结果进行修正。这种利用平滑值对时间序列的线性趋势进行修正，进而建立线性平滑模型预测的方法就是二次指数平滑法，也称线性指数平滑法。它主要用于非季节性且有线性趋势的时间序列。常用的二次指数平滑法有布朗（Brown）单参数指数平滑和霍尔特（Holt）双参数指数平滑。

1. 布朗（Brown）单参数指数平滑

与趋势移动平均法类似，布朗单参数指数平滑的步骤是：首先需要对原始数据进行一次指数平滑，在一次平滑值基础上再进行一次指数平滑，然后根据两次平滑结果建立直线修正模型。

设时间序列为y1 ,y2,…,yt,…,yn，则两次平滑结果为

当时间序列从某一项开始具有直线趋势时，建立直线修正模型

2. 霍尔特（Holt）双参数指数平滑

布朗单参数指数平滑是对序列一次平滑值又进行了一次指数平滑。而霍尔特双参数指数平滑是对序列进行一次平滑，同时对（一次平滑值的）趋势值进行一次平滑，故有两个平滑参数，有很大的灵活性，预测精度往往较高，应用较广泛。

1）预测模型

式（7.7）与式（7.8）分别反映了序列的水平部分与趋势部分，联立可得霍尔特双参数指数平滑法的平滑公式

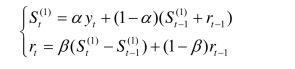
式中：α,β（0＜α,β＜1）为两个平滑系数。使用该方法向前l期（l=1,2,…）的预测模型为

2）相关参数的设定

初始值的设定同简单指数平滑法。另外，同设定一样，初始值r0的设定也有很多种方法，常用的是以下三种方式：

与r0一般对预测模型前几期的影响较大，对后期预测的影响不大，所以用霍尔特指数平滑法进行预测时，最重要是确定平滑系数α与β的取值，这决定了预测的精确程度。

平滑系数α的设定原则与简单指数平滑法一样，β的设定原则与α基本相同，当α取值较大时，β往往不会太小。在实际应用过程中，可以多取几个平滑系数α与β，然后选择预测误差较小的作为最后的预测模型。

3. 实际应用

对于以上提到的二次指数平滑法，在运用SPSS时，同样不需要设定相关参数，系统会自动计算最优解。下面结合SPSS操作解决例1。

例1 表7.4.3给出了1996—2015年我国私有汽车的拥有量数据，试进行分析并预测未来五年的私有汽车拥有量。

表7.4.3　1996—2015年我国私有汽车拥有量　　　　单位：万辆

(www.xing528.com)

解 （1）先绘制时间序列图，如图7.4.7所示。

由序列图可知，后期基本上呈直线趋势，可以考虑用二次指数平滑法进行分析预测。

（2）模型创建。SPSS操作步骤与上述简单指数平滑一样，分为四步，具体不再详述，这里说明有差别的地方。

对于例1中的数据，按前文的步骤②完成后，会出现图7.4.3的对话框。考虑该序列呈现线性趋势，所以在步骤③中不选“简单”，这里选择“霍尔特线性趋势”。

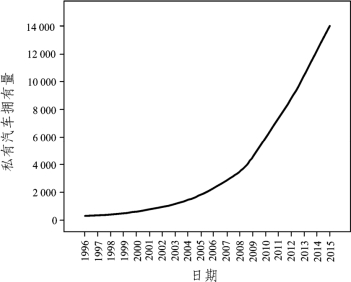
图7.4.7　私有汽车拥有量序列图

步骤④中，对话框中统计再勾选“R方”及“正态化BIC”（具体见图7.4.8），“图”的操作一样，“保存”中可只勾选“预测值”，“选项”中输入日期为“2020”，即预测未来五年的值。

图7.4.8　时间序列建模器对话框

（3）模型结果。

模型统计（见表7.4.4）、指数平滑法模型参数（见表7.4.5）、残差图（见图7.4.9）及序列图（见图7.4.10），在SPSS的编辑页面会出现详细的预测值。（4）模型分析。

表7.4.4　模型统计

表7.4.5　指数平滑法模型参数

图7.4.9　残差序列的自相关图与偏自相关图

图7.4.10　预测值的序列图与实际值序列图

在二次指数平滑中，常用判别系数R2来反映模型拟合的优劣，它表示模型所能解释的数据变异占总变异的比例，数值越大，表示结果越佳。由表7.4.4可知，该模型对应的R2 =0.999，说明该模型拟合非常好，且统计量杨-博克斯Q（18）对应的显著性水平为0.329＞0.05，说明模型拟合后的残差序列不存在自相关或偏自相关，这通过残差图（见图7.4.9）也可以说明。整体拟合效果，也可以从图7.4.10体现出来，其预测值序列图与实际值序列图非常贴合。

对于平滑系数，由表7.4.5可知，Alpha（水平）的值为1，且对应的P值0.006远小于0.05，说明参数Alpha（水平）不仅作用很大而且非常显著；Gamma（趋势）的值也为1，P值为0.063略大于0.05，一般P值小于0.1就可认为有意义，反映了该序列具有趋势特征。模型对应2020年私有汽车拥有量的预测值为24 307.01万辆，这与实际数据24 393万辆很接近。

4. 说明

SPSS中提供了三种二次指数平滑法：霍尔特线性趋势、布朗线性趋势及衰减趋势。衰减趋势也称为阻尼趋势，主要适用于有线性趋势的非季节序列，且该线性趋势正逐渐消失，其结果较保守。相比预测处于快速发展期的事物，它更适合预测处于稳定增长期的事物。

对于二次指数平滑法，在SPSS实际操作时，可依次运行这三种方法，根据R2最大、均方根误差RMSE和正态化BIC最小原则，选择拟合程度最优的模型进行预测。一般先看R2，R2最高者可作为预测模型；当R2相等时，再比较均方根误差RMSE和正态化BIC，（该统计量是基于均方误差的统计量，并考虑了模型的参数个数和序列数据个数），它们高低基本一致，其值越小对应的模型越好。