实用数学方法之趋势移动平均法

1. 基本思想

简单移动平均法和加权移动平均法，在时间序列没有明显的趋势变动时，能够准确反映实际情况。但当时间序列出现线性增加或减少的变动趋势时，用它们来预测就会出现滞后偏差。因此，需要对所得结果进行修正，修正的方法是作二次移动平均，利用移动平均滞后偏差的规律来建立直线趋势的预测模型，这就是趋势移动平均法。

趋势移动平均法的基本思想是：在原始数据基础上，首先进行一次移动平均，得到新的数据列I，然后在此数据基础上再进行一次移动平均，得到数据列Ⅱ，然后根据数据列I和Ⅱ，建立直线模型，对所得数据进行修正。

2. 直线修正模型

设时间序列｛yt｝从某时期开始具有直线发展趋势，且将来一段时期也将按直线趋势变化，设一次直线修正模型为

式中：t为当前时期；l表示预测时期与当前时期的时间差（l=1,2,…,）；yˆt+l为第(t+l)时期的预测值；a t,bt表示直线修正系数。

一次移动平均数为

在一次移动平均的基础上再进行一次移动平均就是二次移动平均，其计算公式为

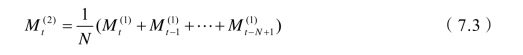
则修正系数为

注：有的把趋势移动平均法称为二次移动平均法，相应的把上面的一次移动平均与二次移动平均称为第一次移动平均与第二次移动平均。

3. 注意事项

（1）当时间序列中后期倾向直线变化时，才能用趋势移动平均法进行分析和预测；

（2）两次移动平均的步长N值必须一致；

（3）两次移动平均的结果不用于预测，而是结合直线修正模型向前预测，即l=1,2,…；

（4）趋势移动平均法可以用于多期预测。

4. 实际应用

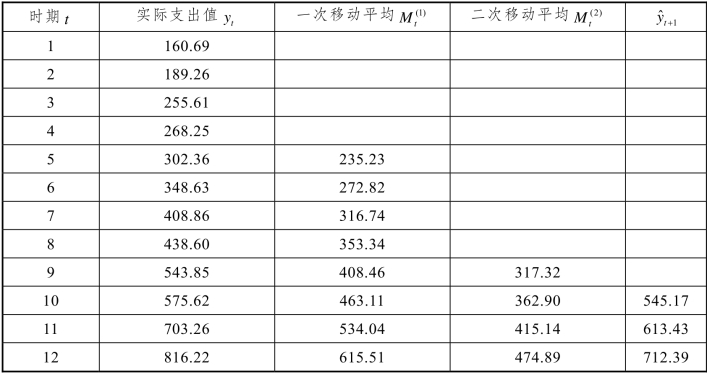
例2 试根据1991—2002年某地禁毒经费统计数据（见表7.3.2）进行预测。

表7.3.2　1991—2002年某地禁毒经费统计数据

解 （1）先绘制时间序列图，如图7.3.5所示，步骤见例1。

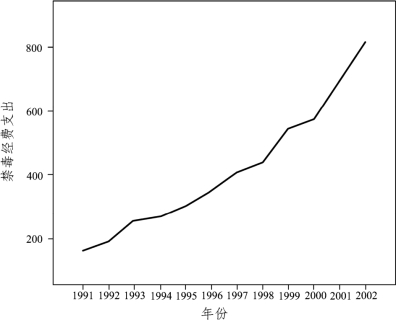
图7.3.5　序列图

由时序图可以看出，1996—2002年禁毒经费支出大致呈直线上升趋势，可以用趋势移动平均法进行预测。

（2）设直线修正模型为

（3）分别取N=4与N=5，并分别计算它们各自对应的一次和二次移动平均值，再代入（7.4）式得到对应的a t,bt，由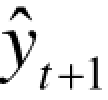=at +bt可得出第t+1期的预测值，见表7.3.3与表7.3.4。

表7.3.3　N=4对应的值

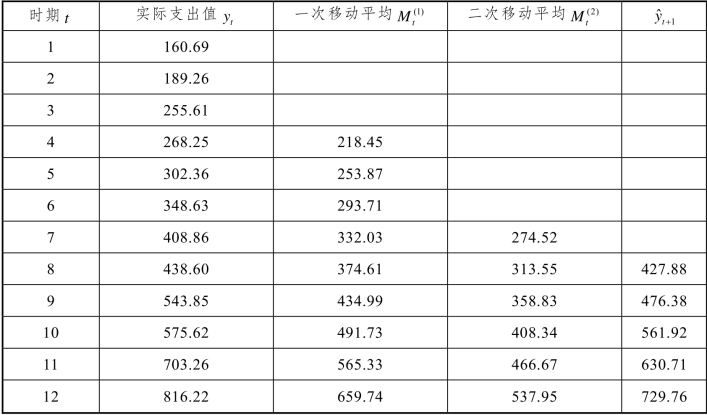
表7.3.4　N=5对应的值

（4）确定模型。分别计算N=4与N=5对应的均方根误差：(www.xing528.com)

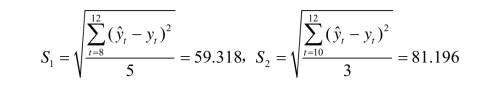
显然，N=4对应的误差较小，取N=4对应的模型为预测模型。

（5）预测2003年与2004年的禁毒经费支出金额。把表7.3.3中的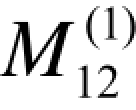和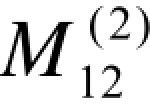代入式（7.4）后，可得a12=781.53,b12=81.19，进而代入直线修正模型

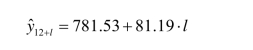
分别令l=1,2，可得2003年与2004年的禁毒经费支出预测金额分别为862.72万元与943.92万元。

另外，趋势移动平均法对于同时存在直线趋势与周期波动的序列，是一种既能反映趋势变化，又可以有效地分离出来周期变动的方法。

例3 表7.3.5给出了2013—2015年四个季度我国从空港出入境的人数（单位：人次），试对该数据进行分析和预测。

表7.3.5　2013—2015年我国从空港出入境的人数

解 （1）先绘制时间序列图，如图7.3.6所示。

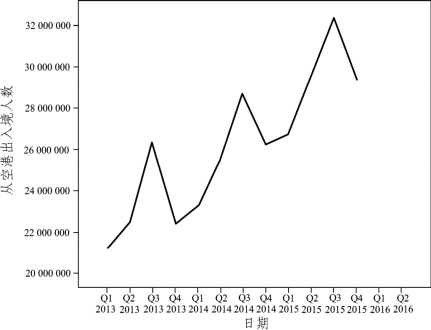
图7.3.6　从空港出入境人数序列图

由时序图可以看出，该组数据既有直线上升趋势，又有季节的周期波动，可以用趋势移动平均法进行分析和预测。显然，应取N=4，表7.3.6给出了其一次与二次移动平均值。

表7.3.6　N=4对应的值

（2）设直线修正模型为

（3）N=4时，由表7.3.6可知

代入修正系数公式，得

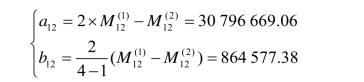
所以修正模型为

（4）预测2016Q1我国从空港出入境的人数。当l=1时，预测值为

取整后，得2016Q1我国从空港出入境人数的预测值为31 661 246。

若不考虑季节因素，只借助序列散点图（见图7.3.7）来判断，则散点呈现带状区域，此时可以考虑线性模型。

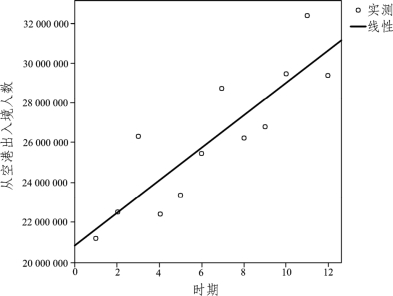
图7.3.7　散点图

由SPSS计算可知，该线性方程为

对应的判别系数R2 =0.76。把t=13代入上式，取整后，可得2016Q1我国从空港出入境人数的预测值为31 511 644。

经查阅，2016Q1我国从空港出入境人数的实际值为32 595 566。上述两种方法对应的预测值的相对误差绝对百分比分别为2.866%、3.325%，虽然这两种方法有些滞后，但趋势移动平均法通过“平滑”可以适当地分离出季节引起的周期变动，其精度更高些。