使用数学方法拟合指数曲线

1. 指数曲线模型

大量研究表明，很多事物的发展在前半时期是按指数或者接近指数规律变化的，例如文献的数量、技术的进步、生产的增长等，即对应的数据增长较快，这种趋势就是指数曲线趋势。若要预测这些事物未来短期内的发展趋势，可对其时间序列进行指数曲线拟合后再预测。常用的有一次指数曲线（y=a·bt ）和二次指数曲线（y =a ·b t·ct 2）。一次指数曲线的拟合被运用得更多些，在时间序列中，对应的指数曲线模型的公式为

其中：yt为时间序列实际观察值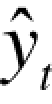；为序列的估计值；t为自变量时间；a,b为模型参数。

由于指数函数可以线性化，那么在实际操作中，参数a,b可通过同上的SPSS操作得到，即在进行到如图7.2.4的步骤时，将对话框中的模型中的“指数”勾选即可。

对上面的例1，我们也可以用指数曲线拟合，大家会发现前期拟合得很好，不过由于指数模型增长较快，后期的预测值偏大。（这个过程大家可自己操作下）

2. 修正指数曲线模型

现实中，任何事物的发展都有一个限度，比如，人口不可能无限制地增长，在一定范围内，一定条件下人口的增长是有限度的；又如，一种新产品投入市场后，需求量不可能无限地增长，而是常常呈现出需求量先是迅速增加，一段时期后逐渐降低增加速度，最后达到市场需求的饱和量。即对初期增长较快、随后增长减缓（或处于稳定发展饱和期）的这种社会现象，不能用一般的指数曲线预测其发展趋势，而需要用特殊的指数曲线模型—— 修正指数曲线模型进行预测。修正指数曲线模型的公式为

曲线y =l -a ·bt的图像如图7.2.7所示。

式（7.1）中的“饱和量”l已知时，把l-yt看作新的时间序列，进而利用操作指数函数的方法可求得参数a,b。

大多情况下，l是未知的，此时该非线性问题属于不能线性化的问题，理论上可利用“三段和值法”（简称三和法）来求得l和a,b。设(t i,y i)(i=1,2,…,n)是一组观测数据，将数据平均分成三组（当数据个数n不是3的倍数时，可舍弃1个或2个数据），按顺序计算每段的“和值”，设为∑1，∑2，∑3，则拟合系数计算公式如下：

图7.2.7　修正指数曲线图

求得以上参数的值后，代入yˆt=l-a·bt 便可得观察值yt的预测值。检验模型拟合程度好坏时，常用平均绝对百分比误差MAPE来检验：

检验对实际值的预测精度高低时，可用预测值的相对误差绝对百分比检验：

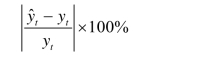
若MAPE为5%，表示预测的平均偏离为5%。简单来说，以上两个值越小越好，究竟小于多少为好，没有统一的标准，这主要与研究的领域和问题有关。通常用它们来比较运用不同方法得到的拟合值（即预测值），值越小表示对应的模型拟合得越好。

实际操作中，一般利用计算机软件（SPSS、MATLAB、SAS等）迭代解出非线性模型中的参数，并用损失函数来衡量模型拟合的好坏。下面我们结合SPSS软件来完成例2。

例2 研究俄罗斯1996—2006年迁出人口的规律，统计数据见表7.2.4。

表7.2.4　俄罗斯1996—2006年迁出人口统计数据

解 （1）先绘制时间序列图。这里运用散点图，对应自变量t1=1，ti+1=ti+1。容易看出符合修正指数曲线的变化规律，可应用修正指数曲线拟合数据。

图7.2.8　时间序列图

（2）设修正指数曲线模型为=l-a·bt ，我们运用SPSS迭代估计出其中的参数。

迭代时关键之一是参数初始值的设置，“好的”初始值可以减少电脑的迭代次数，所以初始值与期望的最终解越接近越好；不合适的初始值可能导致收敛性失败或者导致局部（而不是全局）解的收敛性。

通常可先根据已知信息大致估计参数范围，确定出它们是什么数量级的。若不好确定量级，就多尝试几个初始值，比如，设初始值都是1，SPSS计算后，看是否达到了拟合优度（若默认损失函数为残差平方和，就观察R2的值），如果没有达到，接着以该结果为初始值，再次迭代运算，或者换其他初始值进行运算。总之，要多尝试初始值，并选择对应的“损失函数”较小的。

就例2而言，根据已知信息，我们可大致判断出其数量级。由l是其“饱和值”，根据实际数据和图7.2.8的走势，不妨设l的初始值为1 700 000；由于0＜b＜1，可设其初始值为0.5；把这两个参数的初始值代入方程，对应的自变量t1=1时，用y1代替yˆ1，即288 048 =1700 000 -0.5a，解得a=2 823 904，由于l和b的这两个值都是估计的，不妨设a的初始值为2 500 000。另外，由于SPSS系统默认的初始值的取值范围是-99 999～999 999（超过该范围时，系统会出现如图7.2.9的对话框），我们可把原始数据缩小至1/100，对应的参数l和a的值也缩小至1/100。

图7.2.9　SPSS默认的初始值取值范围(www.xing528.com)

操作时，打开SPSS：

① 选择“分析”→“回归”→“非线性”命令，会出现图7.2.10中左边的对话框。

② 导入因变量（注意，这里的数据是实际数据缩小至1/100后的数据），在模型表达式中输入：l-a*b**VAR001（注意，自变量VAR001是导入的，对应数据为1, 2, …），点击左下方的“参数”后出现图7.2.10中右边的对话框。

图7.2.10　非线性回归对话框

③ 在该对话框中，依次输入表达式中对应的参数及初始值，并点击“添加”，输入完成后，点击“继续”，回到图7.2.10的左边对话框（这时，左下方的参数、右上角的“损失函数与约束条件”及下方的“确定”等都会显现出来）。

④ 点击“确定”，相当于默认的损失函数是残差平方和，且无额外的约束条件，将会把运行结果“迭代历史记录”以表格的形式呈现，显示在迭代17次后终止，对应的最优解为

除此之外，在运行结果中还会出现三个表：参数估算值表（给出了三个参数的估计值、标准误差及95%的置信区间）、参数估算值相关性表及方差分析表（见表7.2.5）。

表7.2.5　方差分析表

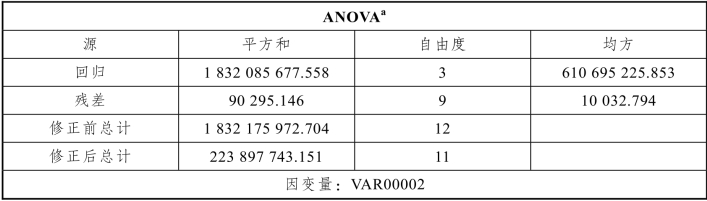
注：a. R2 = 1-（残差平方和）/（修正平方和）= 1.000。

（3）模型检验。对于非线性模型，SPSS是通过最小化损失函数求解和评估模型的，即用损失函数来衡量模型预测的好坏。SPSS默认的损失函数是残差平方和，用户也可以自定义损失函数（输入参数后点击图7.2.10左边对话框中的右上角的损失函数即可），常用的一种自定义损失函数为残差的绝对值，即输入“ABS（RESID_）”，此时，输出结果中只有“迭代历史记录”一个表。

对于该问题，我们没有自定义损失函数，即损失函数为残差平方和，由表7.2.5可知，其结果为90 295.146（该值在“迭代历史记录”表中也会显示），且对应的R 2=1，说明该模型拟合非常好。

（4）写出原数据对应的模型。在运用SPSS计算时，原始数据及对应的参数l和a的值都缩小了1/100，所以把l和a的迭代结果都放大100倍取整后，就可得到原始数据对应的模型表达式，即

且对应的R 2=1，说明该模型拟合程度很“完美”。

（5）可结合实际情况做适当的分析。此处的分析会涉及俄罗斯经济复苏、人们对政府的信心增大、迁出人口已经接近饱和（根据表达式可知，俄罗斯迁出人口数的饱和值为1 921 696）等，有兴趣的读者可以根据实事情况做进一步分析。

以上结果，是在没有添加任何约束条件下得到的。由于0＜b＜1，我们不妨添加该约束条件，即在上述操作步骤③设置好参数后，图7.2.10的左边对话框中的左下方的参数、右上角的“损失函数与约束条件”及下方的“确定”等都会显现出来。这时，点击“约束条件”会出现图7.2.11的对话框，默认的是该对话框上方的“未约束”。

图7.2.11　参数约束对话框

此时，点击“定义参数约束”，把左边添加约束条件的参数“b（0.5）”导入右边的框，在“＜=”后面输入“l”，点击“添加”；再导入b，点击“＞=”后输入“0”，点击“添加”，就得到图7.2.11；点击“继续”，会关闭该对话框，并出现图7.2.12中的对话框，即添加了约束条件后，SPSS的迭代算法改为二次规划算法，原来没有添加约束条件时，系统默认的算法是“利文贝格-马夸特算法”。

图7.2.12　更改算法提示对话框

对图7.2.12中的对话框点击确定，就会回到图7.2.10左边的对话框，点击“确定”，可得运行结果。在“迭代历史记录”表中显示迭代50次后，得到最优解为

默认的损失函数残差平方和最后为22 864 365.112，且对应的方差分析表见表7.2.6。

表7.2.6　方差分析表

注：a. R2=1-（残差平方和）/（修正平方和）=0.898。

由表7.2.5与表7.2.6可知，前者的损失函数—— 残差平方和较小，且前者R2 =1，后者R2 =0.898，所以前者拟合更好。由此可见，添加了约束条件后，结果不一定较好。在实际操作中，知道某个参数的约束范围时，最好在没有约束条件及添加约束条件两种情况下都进行运算，比较哪个结果更好。