实用数学方法：动态经济系统蛛网模型

在市场经济中，一方面，有关商品的价格是由市场上该商品的供应量决定的，供应量越大，价格就越低。另一方面，生产者提供的商品数量又是由该商品的价格决定的，这就导致了市场经济中商品的数量与价格的震荡，即当供大于求的时候会导致价格的下降，价格的下降导致产量的减少，产量的减少又会导致供不应求，商品的供不应求导致商品价格的上涨，这时候又会增加产量，产量的增加又会导致供大于求，数量与价格就在此之间震荡。这种震荡越小越好，震荡太大将会影响人民群众的正常生活。

现在要解决的问题是：

（1）商品数量与价格的振荡在什么条件下趋向稳定?

（2）当不稳定时政府能采取什么干预手段使之稳定?

本节先用图形方法建立所谓“蛛网模型”，对上述问题进行分析，再用差分方程理论建模，对结果进行解释，讨论市场经济趋于稳定的条件，然后作适当推广。

1. 蛛网模型

记xk表示第k时段商品数量，yk表示第k时段商品价格，这里我们把时间离散为时段，1个时段相当于商品的1个生产周期。设

即k时段商品价格取决于同时段的商品数量kx，它反映消费者对这种商品的需求函数关系，称为需求函数。显然，数量越多，价格越低，所以在图4.7.1中用一条下降曲线f表示它，f称为需求曲线。设

即在k+1时段商品数量由第k时段商品价格yk决定，它反映生产者的供应关系，称为供应函数。因为价格越高，生产量越大，在图4.7.1中用一条上升曲线g表示它，g称为供应曲线。

设需求曲线f与供应曲线g相交于点P0 (x0 ,y0)，P0是平衡点。其意义是，一旦在某一时段k有xk =x0，则由式（4.39）、式（4.40），可知yk =y0，xk+1=x0，yk+1=y0，…，即k时段以后商品的数量和价格将永远保持在点P0 (x 0,y0)。但在实际生活中的种种干扰使得数量和价格不可能停止在点P0 (x 0,y0)，不妨设x1偏离x0。我们分析随k的变化，xk和yk的变化。

商品数量x1给定后，由式（4.39）可得y1，进而由式（4.40）可得x2，再由式（4.39）的y2，这样得到一系列的点P1 (x1 ,y1), P2 (x 2,y1), P3 (x 2,y2), …，在图4.7.1中这些点将按箭头所示方向趋向P0 (x0 ,y0)，表明P0是稳定的平衡点，意味着市场经济（商品的价格与数量）将趋向稳定。

但是如果需求函数与供应函数由图4.7.2的曲线所示，市场经济将按照1P，2P，3P，…的规律变化而远离0P，则0P是不稳定的平衡点。意味着商品的价格与数量将出现越来越大的震荡。

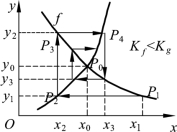
图4.7.1　P0是稳定平衡点

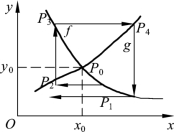
图4.7.2　P0是不稳定平衡点

图中，折线P1 ,P2 ,P3 ,P4…形似蛛网，所以这种用需求曲线和供应曲线分析市场经济稳定性的图示法在经济学中称蛛网模型。实际上，需求曲线f和供应曲线g的具体形式通常是根据各个时段商品的数量和价格的一系列统计资料得到的。

一旦需求曲线和供应曲线被确定下来，商品价格和数量是否趋于稳定。就完全由这两条曲线在平衡点0P附近的形状决定。只要分析图4.7.1和图4.7.2的不同之处就会发现，在0P附近，图4.7.1的f比g陡峭。记f在0P点的斜率的绝对值为Kf，g在0P点的斜率的绝对值为Kg，图形直观告诉我们，当

时0P点是稳定的；当

时0P点是不稳定的。

为了进一步分析这种现象，下面给出蛛网模型的另一种表达式—— 差分方程。

2. 差分方程模型

在0P点附近可以用直线来近似曲线f和g，即

需求曲线f：

供应曲线g：

消去yk，可得一阶线性差分方程

(www.xing528.com)

因此0x是其平衡点，即0P是平衡点。对式（4.45）进行递推，得

由此可得

平衡点稳定的条件：

平衡点不稳定的条件：

3. 模型解释

基于问题（1）的分析：

首先要考虑αβ，的含义，α为商品数量减1单位，价格上涨幅度；β为价格上涨1单位（下时段），供应的增量。所以α是消费者对需求的敏感程度，就是说α小，有利于经济的稳定。β是生产者对价格的敏感程度，就是说β小，有利于经济的稳定。由αβ，和上述求解的模型知，当αβ＜1时，经济就是稳定的，否则经济是不稳定的。

基于问题（2）的分析：

面对经济不稳定的情况，政府应该如何去做？由模型的求解可知，影响经济的稳定性情况是αβ，这两因素，只要把αβ，这两因素的其中一个调小，或者两个一起调小，就可以让经济趋于稳定。

方法一：使α尽量小，如α=0，则需求曲线变为水平。α=0，即政府可以以行政手段控制商品价格不变。

方法二：使β尽量小，如β=0，则供应曲线变为竖直。β=0，即政府可以靠经济实力控制商品数量不变。

4. 模型推广

假如生产者的素质和管理水平更高一些，他们决定商品价格数量，不是根据前一时期的价格，而是根据前两个时期的价格。不妨设

为二者的平均值的函数。相应的式（4.40）的表达式（4.44）修改为

其中：β是平均价格上涨1个单位时xk+1的增量。

设需求函数不变

得到二阶线性常系数差分方程

由方程（4.52）的特征根

可以算出

要使特征根在单位圆内，必须满足

这就是0P稳定的条件。与原有模型中0P点稳定的条件（4.47）相比，参数α,β的范围放大了。这是因为管理者水平和素质的提高，对市场经济稳定起着有利影响的必然结果。