简化的数学工具：SIR模型

大多数传染病如天花、流感、肝炎、麻疹等治愈后均有很强的免疫力，所以病愈的人既非健康者（易感染者），也非病人（已感染者），因此他们将被移除传染系统，我们称之为移除者（Removed），记为R类。

1. 模型假设

假设（1）：总人数N不变，人群分为健康者、病人和病愈免疫的移出者三类，称为SIR模型。时刻t三类人在总人数N中所占的比例分别记为s(t)，i(t)和r(t)。

假设（2）：病人的日接触率为λ，日治愈率为μ（与SI模型相同），传染期接触数为

2. 建模与求解

在假设（1）中显然有

对于病愈免疫的移出者的数量应为

s（s＞），i（0i0＞0），则由式（4.16）、式（4.20）、式（4.21），SIR模型可用微分方程组表示为

不妨设初始时刻的健康者、染病者的比例分别为00 0

s(t)，i(t)的求解非常困难，在此，我们先作数值计算来预估s(t)，i(t)的一般变化规律。

3. 数值计算

在方程(4.11)中设λ=1，μ=0.3，i(0)= 0.02，s(0)=0.98，用MATLAB软件编写程序：

输出的简明计算结果列入表4.3.1中。i(t)，s(t)的图形如图4.3.7所示。图4.3.8是i～s图形，称为相轨线，初值i(0)=0.02，s(0)=0.98相当于图4.3.8中的P0点，随着t的增加，(s,i)沿轨线自右向左运动。由表4.3.1、图4.3.7、图4.3.8可以看出，i(t)由初值增长至t=7时达到最大值, 然后减少，t→∞, i→0, s(t)则单调减少，t→∞，s→0.039 8。

表4.3.1　i(t), s(t)的数值计算结果

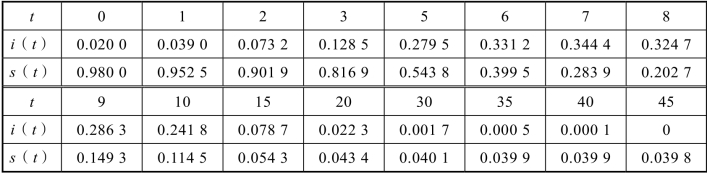
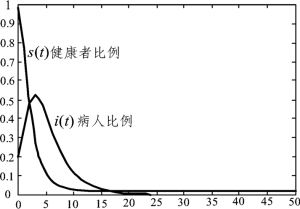
图4.3.7　s(t),i(t)病人比例图

(www.xing528.com)

图4.3.8　i～s图形

为了分析i (t ),s (t)的一般变化规律，需要进行相轨线分析。

4. 相轨线分析

我们在数值计算和图形观察的基础上，利用相轨线讨论解i (t ),s (t)的性质。

s ～i平面称为相平面，相轨线在相平面上的定义域(s,i)∈D为

在方程（4.22）中消去dt并注意到σ的定义，可得

容易求出方程（4.24）的解为

在定义域D内，式（4.25）表示的曲线即相轨线，如图4.3.9所示。其中，箭头表示随着时间t的增加，s(t)和i(t)的变化趋向。

下面根据式（4.22）、式（4.25）和图4.3.9分析s(t)，i(t)和r(t)的变化情况（t→∞时，它们的极限值分别记作s∞，i∞和r∞）：

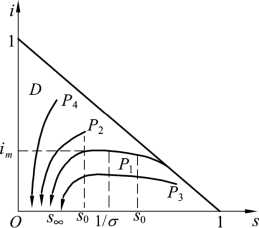
图4.3.9　相轨线

（1）不论初始条件s0，0i如何，病人将消失，即t→∞，i→0。

（2）最终未被感染的健康者的比例是s∞，在式（4.25）中令i=0，得到s∞是方程

5. 群体免疫和预防

这就是说，只要通过群体免疫控制初始时刻的移出者比例（即免疫比例）就可以制止传染病的蔓延。

这种办法生效的前提条件是免疫者要均匀分布在全体人口中，实际上这是很难做到的。据估计，当时印度等国天花传染病的接触数σ=5，至少要有80%的人接受免疫。据世界卫生组织报告，即使花费大量资金提高0r，也因很难做到免疫者的均匀分布，使得天花直到1977年才在全世界根除。而有些传染病的σ更高，其根除就更加困难。