《实用数学方法》中的遗传算法：高效搜索参数空间

1. 遗传算法简介

遗传算法（Genetic Algorithm，GA）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。它是由美国的J. Holland教授于1975年首先提出的，其主要特点是直接对结构对象进行操作，不存在求导和函数连续性的限定；具有内在的隐式并行性和更好的全局寻优能力；采用概率化的寻优方法，不需要确定的规则就能自动获取和指导优化的搜索空间，自适应地调整搜索方向。

遗传算法以一种群体中的所有个体为对象，并利用随机化技术指导对一个被编码的参数空间进行高效搜索。其中，选择□交叉和变异构成了遗传算法的遗传操作；参数编码□初始群体的设定□适应度函数的设计□遗传操作设计□控制参数设定五个要素组成了遗传算法的核心内容。

2. 遗传算法的执行过程

遗传算法是从代表问题可能潜在的解集的一个种群开始的，而一个种群则由经过基因编码的一定数目的个体组成。每个个体实际上是染色体带有特征的实体。

染色体作为遗传物质的主要载体，即多个基因的集合，其内部表现（即基因型）是某种基因组合，它决定了个体的形状的外部表现，如黑头发的特征是由染色体中控制这一特征的某种基因组合决定的。因此，在一开始需要实现从表现型到基因型的映射即编码工作。由于仿照基因编码的工作很复杂，我们往往要进行简化，如二进制编码。

初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代演化产生出越来越好的近似解，在每一代，根据问题域中个体的适应度大小选择个体，并借助于自然遗传学的遗传算子进行组合交叉和变异，产生出代表新的解集的种群。

这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境，末代种群中的最优个体经过解码，可以作为问题近似最优解。

3. 遗传算法的过程图解

遗传算法的一般步骤（图2.3.1）是：

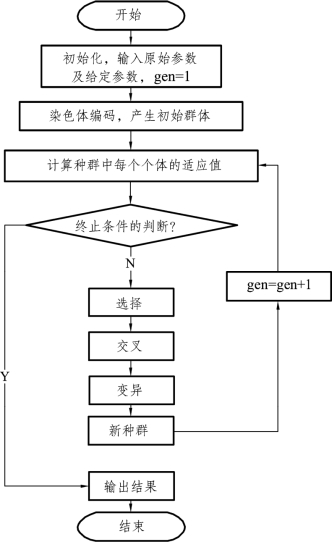
图2.3.1　程序结构框

（1）个体编码（创造染色体）；

（2）产生初始群体（创造初始种群）；

（3）计算适应度（度量物种对于生存环境的适应程度）；

（4）选择运算（基于适应度的优胜劣汰的过程）；

（5）交叉运算（基因重组或杂交）；(www.xing528.com)

（6）变异运算（基因突变）。

4. 问题引出与解决

用MATLAB对遗传算法求函数最大值。

子函数7: 目标函数即为适应度函数targetfun.m

function y=targetfun(x)

%适应度函数, 即原函数

y=200*exp(-0.05*x).*sin(x);

运行结果（见图2.3.2）:

当进化了12代后, x约等于1.5时取到最大值185。

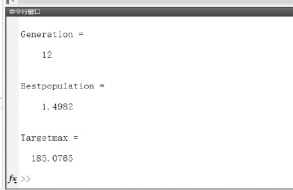
图2.3.2　运行结果窗口