实用数学方法：目标规划求解

1. 图解法

只有两个决策变量的目标规划数学模型，可以使用简单直观的图解法求解。其方法与线性规划图解法类似，先在平面直角坐标系第一象限内做出各约束等式或不等式的图像，然后由绝对约束确定可行域，由目标约束和目标函数确定最优解或满意解。

对于绝对约束，与线性规划中的约束条件画法完全相同。对于目标约束方程，除做出直线外，还要在直线上标出正、负偏差变量的方向，其可行域方向取决于目标函数中对应目标。另外，目标规划是在前一级目标满足的情况下再来考虑下一级目标，尽可能满足目标的解很可能不是可行解（即非可行解），而是权衡以后得出的最优解—— 满意解。因而在目标规划中称求得的解为满意解。

注意：在求满意解的时候，把绝对约束作最高级别考虑。

例5 用图解法求解目标规划问题

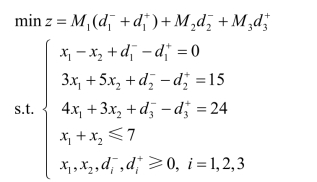
解 在平面直角坐标系第一象限内画出各约束条件的图像（见图2.1.2），目标约束要在直线旁标上di-和di+。

图2.1.2　图解法

所以，线段AB上的所有点为满意解，可求得A（15/8, 15/8），B（24/7, 24/7）。

2. 多目标规划的MATLAB算法

多目标规划可以归结为

其中：x, weight, goal, b, beq, lb和ub是向量；A和Aeq是矩阵；c(x),ceq(x)和F(x)是向量函数，可以是非线性函数。F(x)是所考虑的目标函数，goal是欲达到的目标，则多目标规划的MATLAB函数fgoalattain目标的用法为

[x, fval]= fgoalattain（'fun', x0, goal, weight）

[x, fval]= fgoalattain（'fun', x0, goal, weight, A, b）

[x, fval]= fgoalattain（'fun', x0, goal, weight, A, b, Aeq, beq）

[x, fval]= fgoalattain（'fun', x0, goal, weight, A, b, Aeq, beq, 1b, ub, nonlcon）

其中：fun是用M文件定义的目标向量函数，x0是初值，weight是权重。A, b定义不等式约束A·x≤b，Aeq，beq定义等式约束Aeq·x=beq，nonlcon是用M文件定义的非线性约束c (x)≤0，ceq(x)=0。返回值fval是目标向量函数的值。

要完整掌握其用法，可用 doc fgoalattain和 type fgoalattain 查询相关函数的“帮助”文档。

例6 求解多目标线性规划问题

解 （1）编写M函数Fun.m：

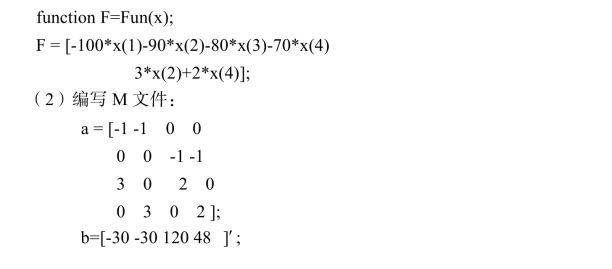
3. 目标规划模型的实例

前面介绍了目标规划的求解方法，这里再介绍几个目标规划模型的例子，以便进一步了解目标规划模型的建立和求解过程。

例7 国内著名的电脑企业生产三种型号的台式电脑A，B，C。这三种型号的台式电脑需要在复杂的装配线上生产组织，生产一台A，B，C型号的电脑分别需要5小时、8小时、12小时。公司装配线正常的生产时间是每月1 700小时，公司营业部门估计A，B，C三种型号的台式电脑的利润分别是每台1 000元、1 440元、2 520元，而公司预测这个月生产的台式电脑能够全部卖出。公司经理考虑以下目标：

第一目标：充分利用正常的生产能力，避免开工不足。

第二目标：优先满足老客户的需求，A，B，C三种型号的电脑分别是50台、50台、80台，同时根据电脑的纯利润分配不同的权因子。

第三目标：限制装配线加班时间，最好不超过200小时。

第四目标：满足各种型号的电脑的销售目标，A，B，C三种型号的电脑分别是100台、120台、100台，再根据三种电脑的纯利润分配不同的权因子。

第五目标：限制装配线加班时间尽可能少。

请列出相应的目标函数。

解 首先建立目标约束。

（1）装配线正常生产。

（2）销售目标。

优先满足老客户的需求，并根据三种型号的电脑的纯利润分配不同的权因子，A，B，C三种型号的电脑的每小时的纯利润是分别200元，180元，210元，因此老客户的销售目标约束为

再考虑一般销售，类似上面的讨论，得

（3）加班限制。(www.xing528.com)

首先，是限制装配线加班时间，不允许超过200小时，得

其次，装配线加班时间尽可能少，即

写出目标规划的数学模型，即

编程计算得到x1=100,x2=55,x3=80。公司装配线生产时间是每月1 900小时，满足装配线加班不超过200小时。能够满足老客户的需求，但未能达到销售目标。销售总利润为

习题2.1

1. 求解多目标线性规划问题

2. 一个小型的无线电广播台考虑如何最好地安排音乐□新闻和商业节目的时间。依据法律，该台每天允许广播12小时，其中商业节目用以盈利，每分钟可收入250美元，新闻节目每分钟需支出40美元，音乐节目每分钟费用为17.50美元。法律规定，正常情况下商业节目只能占广播时间的20%，每小时至少安排5分钟新闻时间。问每天的广播节目该如何安排?优先级如下：

M1：满足法律规定的要求；

M2：每天的纯收入最多。

试建立该问题的目标规划模型。

3. 某工厂生产两种产品，每件产品Ⅰ可获利10元，每件产品Ⅱ可获利8元，每生产一件产品Ⅰ，需要3小时，每生产一件产品Ⅱ需要2.5小时。每周总的有效时间为120小时。若加班生产，则每件产品I的利润降低1.5元，每件产品Ⅱ的利润降低1元。加班时间限定每周不超过40小时，决策者希望在允许的工作及加班时间内取得最大利润，试建立该问题的目标线性模型并求解。

4. 某厂组装两种产品，有关数据如表1所示。要求确定两种产品的日生产计划，并满足：

（1）不得使装配线超负荷生产；

（2）不得有剩余产品；

（3）日产值尽可能达到5 000元。

试找出满意解，并用图示说明。

表1　相关数据

5. 上题中，若将目标要求修改为：

（1）尽可能发挥工厂的装配能力；

（2）尽可能满足市场的需求，并使产量与销量保持一致；

（3）装配生产线可加班，但时数不得超过30小时；

（4）尽可能使日产值最大。

试确定出两种产品满意的日产计划。

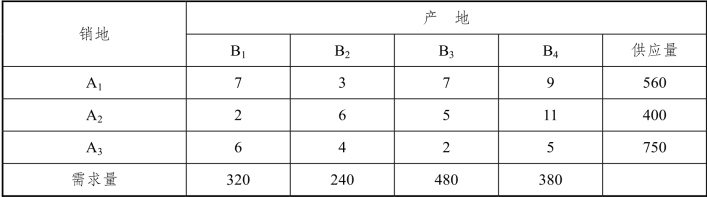
6. 某公司要将一批货从三个产地运到四个销地，有关数据如表2所示。现要求确定调运计划，且依次满足：

（1）B4要保证供应；

（2）其余销地的供应量不低于80%；

（3）A2给B2的供应量不低于150；

（4）A2尽可能少给B1；

（5）销地B1，B2的供应量尽可能保持平衡。

要求：

（1）建立使总运费最小的目标规划模型。

（2）建立该问题的电子表格模型，并用winqsb进行求解。

表2　相关数据

7. 某公司管理层已经为其公司的两种新产品制定了各自的市场目标，具体地说，产品1必须占据15%的市场份额，而产品2必须占据10%的市场份额。为了获得市场，该公司准备开展三次广告活动，其中两个广告是分别针对产品1和产品2的，而广告3是为了提高整个公司及其产品的声誉。以x1 ,x 2,x3分别表示分配在三个广告上的资金（以百万元为单位），相应的两种产品取得的市场份额估计值（以百分比表示）为

广告总预算为5 500万元，其中必须有至少1 000万元投资在第三个广告上。如果两个产品的市场份额目标不能同时实现，管理层认为两种产品上目标偏离的严重性是同等的。在上述条件下，管理层希望得到最有效的资金分配方法，试建立该问题的数学模型。