实用数学方法-目标规划基本概念及模型

1. 基本概念

在这一小节里介绍与目标规划有关的基本概念。

1）偏差变量

对于例1，造成无解的关键在于约束条件太死板。设想把约束条件“放松”，比如占用的人力可以少于70人的话，机时约束和人工约束就可以不再发生矛盾。在此基础上，引入了正负偏差的概念，来表示决策值与目标值之间的差异：

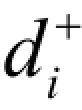—— 正偏差变量，表示决策值超出目标值的部分，目标规划里规定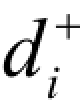≥0；

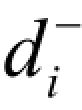—— 负偏差变量，表示决策值未达到目标值的部分，目标规划里规定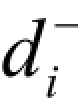≥0。

实际操作中，当目标值（也就是计划的利润值）确定时，所做决策可能出现以下三种情况之一：

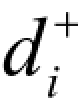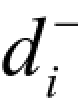（1）决策值超过了目标值（即完成或超额完成计划利润值），表示为≥0，=0；

（2）决策值未达到目标值（即未完成计划利润值），表示为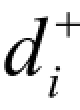=0，≥0；

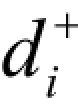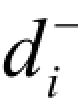（3）决策值恰好等于目标值（即恰好完成计划利润指标），表示为=0，=0。

以上三种情况，无论哪种情况发生，均有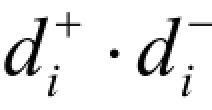=0。

2）绝对（刚性）约束与目标约束

绝对约束也称系统约束，是指必须严格满足的等式约束和不等式约束，如线性规划问题中的所有约束条件，不能满足这些约束条件的解称为非可行解，所以它们是硬约束。

目标约束是目标规划所特有的，可把约束右端项看作要追求的目标值。在达到此目标值时，允许出现正或负的偏差，因此在这些约束中加入了正□负偏差变量，它们是软约束。线性规划问题中的目标函数，在给定目标值和加入正□负偏差变量后可变换为目标约束。

如，例1中假定该企业计划利润值为5 000元，那么目标函数

可变换为

该式表示决策值与目标值5 000之间可能存在正或负的偏差（请读者分别按照上面所讲的三种情况来理解）。

绝对约束也可以根据问题的需要变换为目标约束，此时将约束右端项看作所追求的目标值。如例1中，绝对约束x1+x2 ≤10可变换为目标约束x1 +x 2+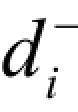-=10。

3）优先次序系数与权系数

一个规划问题往往有多个目标。决策者在实现这些目标时，存在主次与轻重缓急的不同。对于有K级目标的问题，按照优先次序分别赋予不同大小的大M系数：M 1,M2,…,MK ，其中M k(k=1,…,K)为无穷大的正数，并且M1≫M2≫…≫MK（“≫”符号表示“远大于”），这样，只有当某一级目标实现以后（即目标值为0），才能忽略大M的影响，否则目标偏离量会因为大M的影响而无穷放大。由于Mk≫Mk+1，所以只有先考虑忽略Mk的影响（实现第k级目标）后，才能考虑第k+1级目标。实际上，这里的大M是对偏离目标值的惩罚系数，优先级别越高，惩罚系数越大。

权系数ωi用来区别具有相同优先级别的若干目标。在同一优先级别中，可能包含有两个或多个目标，它们的正、负偏差变量的重要程度有所差别，此时可以给正、负偏差变量赋予不同的权系数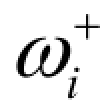和。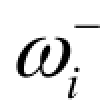

4）目标规划的目标函数(www.xing528.com)

目标规划的目标函数（准则函数）是按各目标约束的正□负偏差变量和赋予相应的优先因子而构造的。对于满足绝对约束与目标约束的所有解，从决策者的角度来看，判断其优劣的依据是决策值与目标值的偏差越小越好。因此，目标规划的目标函数是与正□负偏差变量密切相关的函数，表示为minz =f (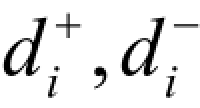)。其基本形式有三种：

（1）第i个目标要求恰好达到目标值，即正□负偏差变量都尽可能地小。此时，构造目标函数为

（2）第i个目标不超过目标值，即允许达不到目标值，正偏差变量尽可能地小。此时，构造目标函数为

（3）第i个目标要求超过目标值，即超过量不限，但必须负偏差变量尽可能地小。此时，构造目标函数为

但对于一个具体的目标规划问题，各级目标的优先次序及权系数的确定由决策者按具体情况给出，以下用例子说明。

例3 在例1中，假定目标利润不少于15 000元，为第一目标；占用的人力可以少于70人，为第二目标。试求决策方案。

解 按决策者的要求分别赋予两个目标大M系数M 1,M2。这个问题的数学模型如下：

例4 某纺织厂生产A□B两种布料，平均生产能力均为1千米/时，工厂正常生产能力是80时/周。又A布料每千米获利2 500元，B布料每千米获利1 500元。已知A□B两种布料每周的市场需求量分别是70千米和45千米。现该厂确定一周内的目标为

第一优先级：避免生产开工不足；

第二优先级：加班时间不超过10小时；

第三优先级：根据市场需求达到最大销售量；

第四优先级：尽可能减少加班时间。

试求该问题的最优方案。

解 设x1,2x分别为生产甲□乙布料的小时数。对于第三优先级目标，根据A□B布料利润的比值2 500:1500=5:3，取二者达到最大销量的权系数分别为5和3。该问题的目标规划模型如下：

综上所述，目标规划建立模型的步骤为：

（1）根据问题所提出的各目标与条件，确定目标值，列出目标约束与绝对约束。

（2）根据决策者的需要将某些或全部绝对约束转换为目标约束，方法是绝对约束的左式加上负偏差变量和减去正偏差变量。

（3）给各级目标赋予相应的惩罚系数Mk（k=1,2,…,K ），Mk为无穷大的正数，且M1≫M2≫…≫MK。

（4）对同一优先级的各目标，再按其重要程度不同，赋予相应的权系数ωkl。

（5）根据决策者的要求，各目标按以下三种情况取值：① 恰好达到目标值，取di++di-；②允许超过目标值，取di-；③不允许超过目标值，取di+。然后构造一个由惩罚系数□权系数和偏差变量组成的□要求实现极小化的目标函数。