实用数学方法解决多目标规划问题

线性规划问题是讨论一个给定的线性目标函数在一组线性约束条件下的最大值或最小值问题。对于一个实际问题，管理科学者根据管理层决策目标的要求，首先确定一个目标函数以衡量不同决策的优劣，且根据实际问题中的资源□资金和环境等因素对决策的限制提出相应的约束条件以建立线性规划模型；然后用计算机软件求出最优方案并作灵敏度分析以供管理层决策使用。而在一些问题中，决策目标往往不止一个，且模型中有可能存在一些互相矛盾的约束条件的情况，用已有的线性规划的理论和方法无法解决这些问题。因此，1961年美国学者查恩斯（A. Charnes）和库柏（W. W. Coopor）提出了目标规划的概念与数学模型，以解决经济管理中的多目标决策问题。

我们将通过几个例子来说明在实际应用中线性规划存在的一系列局限性。

例1 某厂生产A□B两种产品每件所需的劳动力分别为4个人工和6个人工，所需设备的单位台时均为1。已知该厂有10个单位机器台时提供制造这两种产品，并且至少能提供70个人工。已知A□B产品的利润，每件分别为300元和500元。试问：该厂各应生产多少件A□B产品，才能使其利润最大?

解 设该厂能生产A□B产品的数量分别为x1,x2件，则有

图解法求解如图2.1.1所示。

图2.1.1　图解法

由图2.1.1可得，满足约束条件的可行解集为∅，即机时约束和人工约束之间产生矛盾，因而该问题无解。但在实际中，该厂要增加利润，不可能不生产A□B两种产品，而由线性规划模型无法为其找到一个合适的方案。(www.xing528.com)

例2 某厂为进行生产需采购A□B两种原材料，单价分别为70元/千克和50元/千克。现要求购买资金不超过5 000元，总购买量不少于80千克，而A原材料不少于20千克。问如何确定最优的采购方案（即花费的资金最少，购买的总量最大）?

解 这是一个含有两个目标的数学规划问题。设x1,x2分别为购买两种原材料的千克数，f1 （x1 ,x2）为花费的资金，f 2（x1 ,x2）为购买的总量。建立该问题的数学模型如下：

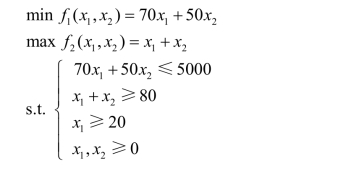
对于这样的多目标问题，很难用线性规划找到最优方案。极可能的结果是，第一个方案使第一目标的结果值优于第二方案，同时第二方案使第二目标的结果值优于第一方案，也就是说很难找到一个一致最优方案，使两个目标的函数值同时达到最优。另外，对于多目标问题，还存在不同目标的重要程度一样的问题，而这也是线性规划所无法解决的。

在线性规划的基础上，建立了一种新的数学规划方法—— 目标规划法，用于弥补线性规划的上述局限性。总的来说，目标规划和线性规划的不同之处可以从以下几点反映出来：

（1）线性规划只能处理单个目标，而现实问题往往存在多个目标。目标规划能统筹兼顾地处理多个目标的关系，求得切合实际需求的解。

（2）线性规划是求满足所有约束条件的最优解。而在实际问题中，可能存在相互矛盾的约束条件而导致无可行解，但此时生产还得继续进行。即使存在可行解，实际问题中也未必一定需求出最优解。目标规划是要找一个满意解，即使在相互矛盾的约束条件下也找到尽量满足约束的满意解，即满意方案。

（3）线性规划的约束条件是不分主次地等同对待，这并不都符合实际情况。而目标规划可根据实际需要给予轻重缓急的考虑。