用实例演示非线性规划方法

下面介绍一个非线性规划的实例—— 飞行管理问题，这是1995年全国大学生数学建模竞赛的A题。

1. 问题的提出—— 飞行管理问题

在约10km高空的某边长160km的正方形区域内，经常有若干架飞机水平飞行。区域内每架飞机的位置和速度向量均由计算机记录其数据，以便进行飞行管理。当一架欲进入该区域的飞机到达区域边缘时，记录其数据后，要立即计算并判断是否会与区域内的飞机发生碰撞。如果会碰撞，则应计算如何调整各架（包括新进入的）飞机飞行的方向角，以避免碰撞。现假定条件如下：

（1）不碰撞的标准为任意两架飞机的距离大于8 km；

（2）飞机飞行方向角调整的幅度不应超过30°；

（3）所有飞机飞行速度均为800 km/h；

（4）进入该区域的飞机在到达区域边缘时，与区域内飞机的距离应在60 km以上；

（5）最多需考虑6架飞机；

（6）不必考虑飞机离开此区域后的状况。

请对这个避免碰撞的飞行管理问题建立数学模型，列出计算步骤，对以下数据进行计算（方向角误差不超过0.01°），要求飞机飞行方向角调整的幅度尽量小。

设该区域4个顶点的坐标为(0, 0)，(160, 0)，(160, 160)，(0, 160)，记录数据见表1.3.1。

表1.3.1　飞行记录数据

注：方向角指飞行方向与x轴正向夹角。

2. 模型的分析和假设

（1）α为飞机飞行速度，α=800km/h；

（2）D为飞行管理区域的边长；

（3）Ω为飞行管理区域，其坐标为(0, 0)，(160, 0)，(160, 160)，(0, 160)；

（4）(xi 0,yi0,θi 0)为第i架飞机的初始位置及初始方向角，i=1,2,…,6，i=6为新进入的飞机；

（5）(xi (t ),yi (t))为第i架飞机的在t时刻的位置；

（6）Δθi为第i架飞机的方向角的调整量，根据条件，应满足且调整后的方向角θi=θi0+Δθi。

3. 模型的建立

模型一 根据相对运动原理，在任意时刻两架飞机i和j的相对飞行速度为

在t时刻两架飞机i和j的相对位置为

在t时刻两架飞机i和j的相对距离为

根据不碰撞的标准为任意两架飞机的距离大于8km，则有非线性规划模型：

模型二 将相对飞行速度化简可得

初始时刻两架飞机i和j的相对距离为

(www.xing528.com)

根据不碰撞的标准为任意两架飞机的距离大于8 km，则有

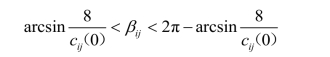
因此两架飞机不碰撞的条件为

其中：ijβ°为调整前这两架飞机的相对飞行方向角。

根据题目要求，得到非线性规划模型：

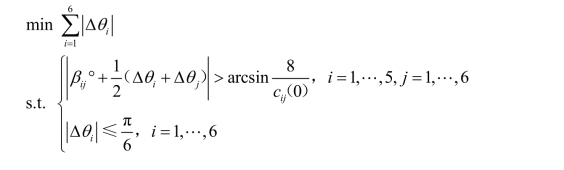
4. 模型的求解

模型一 求解：

在模型一中，有参数t，一种简单的求解方法是将t离散化，给出t的r个确定的值，得

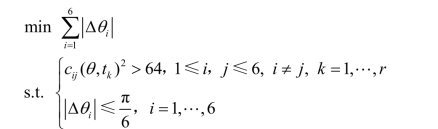
从而求得原规划的最优解Δθ3=2.120 3°，Δθ4=-0.4701°，Δθ6=1.649 2°，其他调整角度为0，总的调整角度之和为4.239 9°。

模型二 求解：

通过MATLAB求解得Δθ3 =2.838 6°，Δθ6 =0.790 8°，其他调整角度为0，总的调整角度之和为3.629 4°。

5. 结果的分析

模型二的总的调整角度之和比模型一的少0.610 5°，所以模型二优于模型一。

习题1.3

1. 求解下列非线性规划问题

2. 求解下列非线性规划问题

3. 用罚函数法求解飞行管理问题的模型一。

4. 建立模型并求解以下问题。

问题1：

一家石油公司现有5 000桶A类原油和10 000桶B类原油。公司销售两种石油产品：汽油与民用燃料油。两种产品由A类原油和B类原油化合而成。每种原油的质量指数如下：A类原油为10，B类原油为5。汽油的质量指数至少为8，民用燃料油至少为6。每种产品的需求量与该产品的广告有关：1美元的广告费可以带来5桶的汽油需求量，或者10桶的民用燃料油需求量。汽油的售价是每桶25美元，民用燃料油的售价为每桶20美元。建立相应的数学模型，帮助公司获得最大利润。（假定没有其他类型的产品可以购买）

问题2：

考虑问题1，并作如下修正：假定我们添加称为SQ的化学添加剂来改善汽油和民用燃料油的质量指数。如果在每桶汽油中添加x量的SQ，则汽油的质量指数将比原指数提高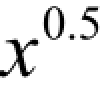，如果在每桶民用燃料油中添加x量的SQ，则民用燃料油的质量指数将比原指数提高0.6x0.6。加到民用燃料油的SQ不能超过原体积的5%，类似地，加到汽油的SQ也不能超过原体积的5%。SQ可以在市场上买到，其售价为每桶20美元。

问题3：

考虑问题2，并作如下修改：在购买400桶SQ后，每桶SQ的价格可以折扣10美元。

注1：x桶的A类原油与y桶的B类原油混合，其质量指数为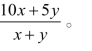

注2：汽油（或民用燃料油）的体积将随着SQ的添加而增加。