0-1整数规划是整数规划中的特殊情形,它的变量xj仅取值0或1。这时,xj称为0-1变量,或称二进制变量。xj仅取值0或1这个条件可表述为如下约束条件:它和一般整数规划的约束条件形式是一致的,因此可以采用一般的整数规划方法求解0-1整数规划。下面先介绍引入0-1变量的实际问题。
![]()
1. 关于固定费用的问题
例3 某产品有几种不同的生产方式。一般,如所选的生产方式投资高(如选购自动化程度高的设备),由于产量大,分配到每件产品的变动成本反而较低;反之,如选定的生产方式投资低,则分配到每件产品的变动成本就有可能增加。所以,必须综合考虑。设xj表示采用第j种方式时的产量;cj和kj分别表示采用第j种方式时每件产品的变动成本和固定成本,这里j = 1, 2, 3。为了说明成本的特点,暂不考虑其他约束条件。采用各种生产方式的总成本分别为
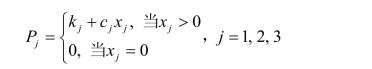
引入0-1变量y j (j=1,2,…,m),当采用第j种生产方式时yj=1,其余时候为0,于是目标函数为
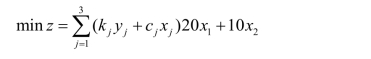
关于yj的取值规定也可以表述为
![]()
其中:M是足够大的正常数。上式说明,当xj >0时,yj =1;当xj =0时,yj=0。
2. 相互排斥的约束条件
例4 某厂拟用集装箱采用车或船托运甲、乙两种货物,两种方式下每箱的体积、质量、获利及托运条件分别如表1.2.1和表1.2.2所示。两种托运方式只能选择一种,问应如何安排托运两种货物,才能使获利最大?
表1.2.1 车运两种货物

表1.2.2 船运两种货物

解 设x1,2x分别表示托运甲、乙两种货物的箱数,如果选择车运,其模型为
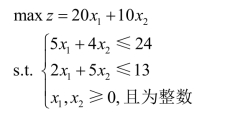
如果选择船运,则其模型为
 (https://www.xing528.com)
(https://www.xing528.com)
因为这两种托运方式是相互排斥的,只能选择一种。为了将它们统一在一个模型中,现在引入0-1变量y,令

约束条件改为

其中:M为充分大的数。当y=0时,每一组的第一个约束条件成立,则退化为车运的约束条件,第二个约束条件自然成立,因而是多余的;反之,当y=1时,第二个约束条件成立,则退化为船运的约束条件,第一个约束条件自然成立,因而是多余的。
一般来说,如果有m个互相排斥的约束条件
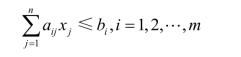
为保证这m个约束条件只有一个成立,可通过引入0-1变量y i(i=1,2,…,m)和一个充分大的数M,则下述m+1个约束条件
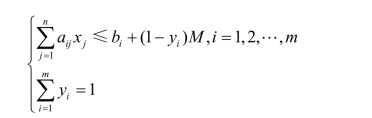
可满足要求。在这m个yi中只能有一个为1,其余都为0,因此只有这一个约束条件成立,其余都是多余的。
3. 关于相互排斥的决策问题
例5 某市在A、B、C、D四个区要建立消防站,共有10个地点可供选择,记为Ai ,i=1,2,…,10。具体情况如表1.2.3所示。
表1.2.3 消防站备选地点

如果选择Ai点,相应的投资为bi万元,每年的利润为ci万元,投资总额不超过M万元。如何安排才能使每年的利润最大?
解 设xi(i=1, 2, …, 10)为0-1变量,其取值为
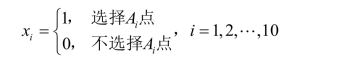
此模型可表述为
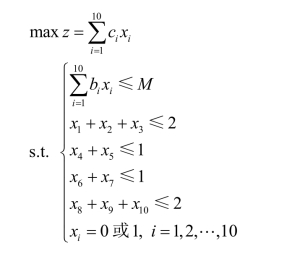
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




