n维向量空间及基变换与坐标变换解析

【主要内容】

1.向量空间与n维向量空间的概念

（1）向量空间

设V是同维向量的非空集合，且对向量的加法和数乘这两种运算是封闭的，则称V是向量空间.

（2）n维向量空间

设V是向量空间，如果V中存在线性无关向量组ε₁，ε₂，…，ε_n，且V中的任一向量都可由这个向量组线性表示，则称V是n维向量空间，记为Vⁿ，称ε₁，ε₂，…，ε_n为V的一组基.显然Vⁿ中任一向量x，对ε₁，ε₂，…，ε_n的线性表达式是唯一的，记为

x=x₁ε₁+x₂ε₂+…+x_nε_n，（1）称x₁，x₂，…，x_n是x在基ε₁，ε₂，…，ε_n下的坐标，式（1）也可记为

2.基变换与坐标变换

（1）基变换

设n维向量空间Vⁿ中有两组基ε₁，ε₂，…，ε_n和η₁，η₂，…，η_n，且

即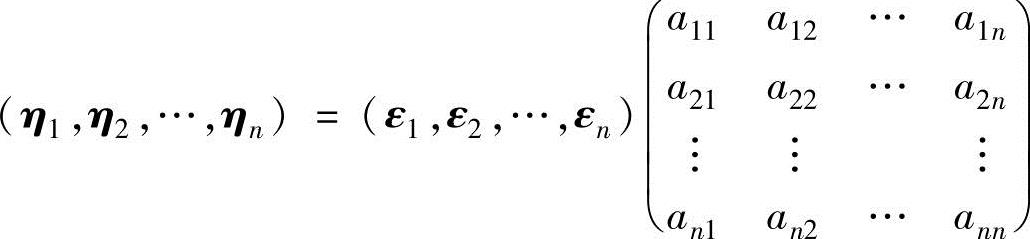，则称它们为由基ε₁，ε₂，…，ε_n到基η₁，η₂，…，η_n的基变换，称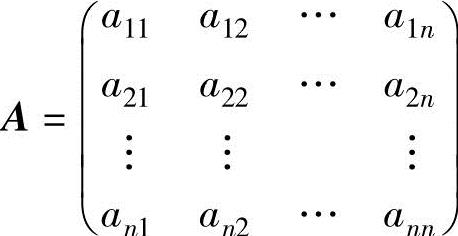为由基ε₁，ε₂，…，ε_n到基η₁，η2，…，η_n的过渡矩阵.

过渡矩阵有以下性质：

（ⅰ）设ε₁，ε₂，…，ε_n与η₁，η2，…，ηn是Vⁿ的两组基，则基ε₁，ε₂，…，ε_n到基_η1，η2，…，ηn的过渡矩阵是n阶可逆矩阵.

（ⅱ）设ε₁，ε₂，…，ε_n与η₁，η2，…，ηn是Vⁿ（在其中定义了内积）的两组单位正交基（即ε₁，ε₂，…，ε_n与η₁，η2，…，ηn都是单位正交向量组），则基ε₁，ε₂，…，ε_n到基_η1，η2，…，ηn的过渡矩阵是n阶正交矩阵.

（2）坐标变换

设Vⁿ的向量x在基ε₁，ε₂，…，ε_n和基η₁，η₂，…，η_n下的坐标分别为x₁，x₂，…，x_n和y₁，y2，…，yn，即

且基ε₁，ε₂，…，ε_n到基η₁，η2，…，ηn的过渡矩阵为A，则x₁，x₂，…，x_n与y1，y₂，…，yn之间有以下关系，或

【典型例题】

例5.10.1 求在3维向量空间中，从基α₁=（1，1，1）T，α₂=（1，0，-1）T，α₃=（1，0，1）T到β₁=（1，2，1）T，β₂=（2，3，4）T，β₃=（3，4，3）T的过渡矩阵A.(www.xing528.com)

精解 由过渡矩阵的定义知

（β₁，β2，β3）=（α1，α2，α3）A，

即

由于

所以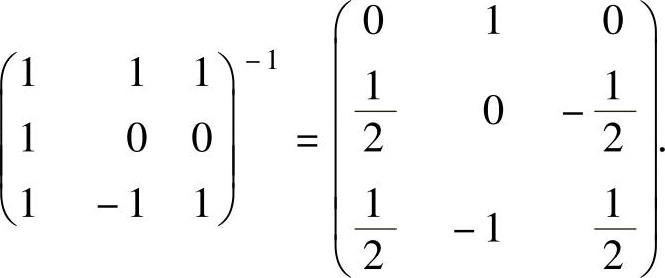将它代入式（1）得基α₁，α₂，α₃到基β₁，β₂，β3的过渡矩阵为

例5.10.2 设α₁，α₂，α₃是3维向量空间的一组基，求由基α₁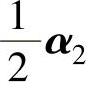，，到基α₁+α₂，α2+α₃，α3+α1的过渡矩阵A.

精解 不妨设α₁，α₂，α₃都是3维列向量，则按过渡矩阵的定义知

即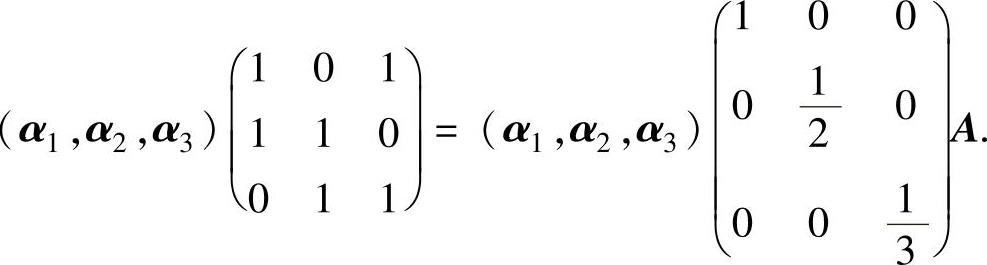

由于（α₁，α₂，α₃）是三阶可逆矩阵，所以上式可以化简为

即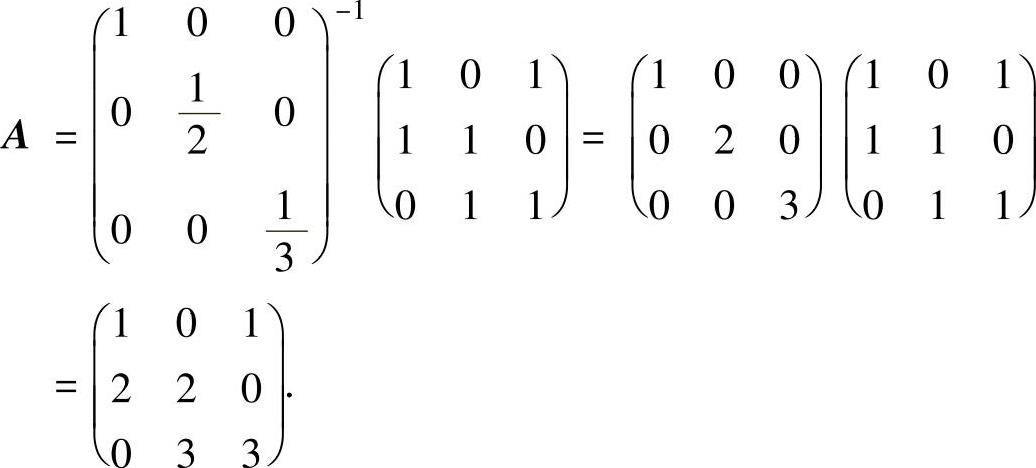例5.10.3 设ε₁，ε₂，ε₃是3维向量空间V³的一组单位正交基，证明：

也是V³的一组单位正交基.

精解 只要证明即可.

同理可以证明

（η₁，η3）=（η2，η3）=0.

此外，

同理可以证明

（η₂，η2）=（η3，η3）=1.因此，η₁，η2，η3也是V³的一组单位正交基.