牛顿第二定律求质点运动规律

【主要内容】

质量为m的质点，在外力F（t）的作用下沿直线运动，记其运动规律为x=x（t），则由牛顿第二定律知，x（t）满足微分方程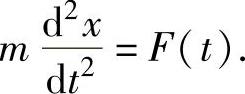

于是求解上述微分方程可得满足初始条件x（t₀）=x₀，x′（t₀）=x₁的运动规律x=x（t）（t≥t₀）.

【典型例题】

例附3.1 一质量为m=0.5kg的爆竹，由初速v₀铅直向上飞向高空.已知在上升过程中，空气对它的阻力与它的运动速度v的平方成正比，比例系数为k（0<k<1）.求从起爆点算起该爆竹能够到达的最大高度.

精解 设爆竹的运动规律为h=h（t）（其中h（t）是从起爆时刻t=0开始计算的，在t时刻爆竹的高度），则由牛顿第二定律得

令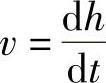，则上式成为

即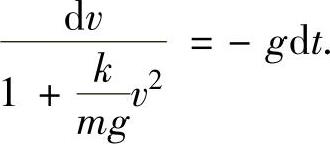它的通解为

将初始条件v（0）=v₀代入通解得代入上式得

显然，满足v（t）=0的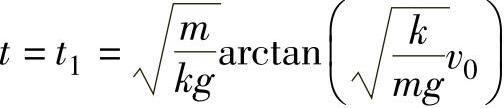是爆竹达到最高点的时刻，于是爆竹能够达到的最大高度为

例附3.2 某种飞机在机场降落时，为了减少滑行距离，在触地的瞬间，飞机尾部张开减速伞，以增大阻力，使飞机迅速减速并停下.

现有一质量m=9000kg的飞机，着陆时的水平速度为v₀=700km/h.经测试，减速伞打开后，飞机所受的总阻力与飞机的速度成正比（比例系数为k=6.0×10⁶），问从着陆点算起，飞机滑行的最长距离是多少（注：kg表示千克，km/h表示千米/时）？

精解 用x（t）表示时刻t飞机的滑行距离（从飞机着地开始计时和计距）.利用力学中的牛顿第二定律建立以x（t）为未知函数、t为自变量的微分方程，求出x（t）的表达式，由此即可求得飞机滑行的最长距离.

根据题设，利用力学中的牛顿第二定律得(www.xing528.com)

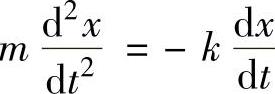，即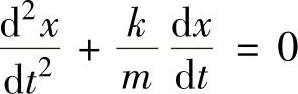 （二阶常系数齐次线性微分方程），

它的通解为

由题设知，x_t=0=0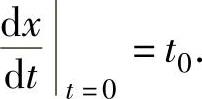，将它代入式（1）得

解此方程组得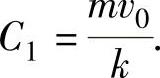将它代入式（1）得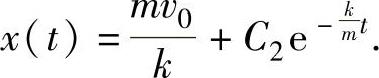由此得到飞机滑行的最长距离为

图附 3.3

例附3.3 长为81cm的匀质链条，从水平桌面上滑下，其初速度为零.设其中有49cm是垂直于桌子边缘的直线状态位于桌面上，另有32cm垂直于桌面下方（见图附3.3）.设桌面与链条之间的摩擦系数为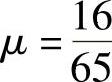，求该链条全部从桌面滑下所需的时间.

精解 作坐标系如图附3.3，x（t）表示在时刻t时从链条开始下滑计时，链条下垂部分端点的坐标.建立以x=x（t）为未知函数、t为自变量的微分方程.解此微分方程即可以算出该链条全部滑下所需的时间.设链条的质量为m，则由题设知其所受的力为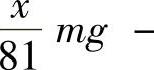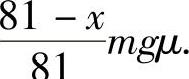于是由力学中的牛顿第二定律得

即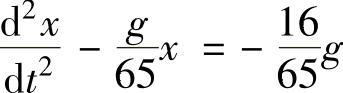（二阶常系数线性微分方程）.

它的通解为

由题设知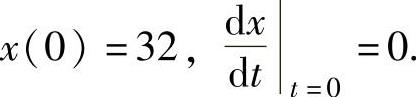将它代入式（1）得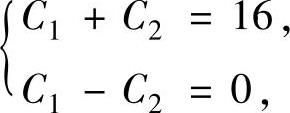即C₁=C₂=8.

将它代入式（1）得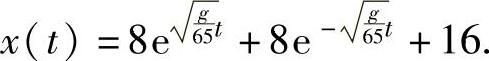令x（t）=81，即

解此方程得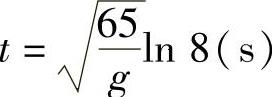，这就是链条全部滑下桌面所需的时间.