求解引力和水的侧压力

【主要内容】

1.引力

面密度为ρ（x，y）的薄片D对不在D上的质量为m的质点A（x₀，y₀）的引力为

其中，r=（x-x₀）i+（y-y₀）j，其模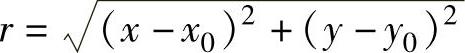，G为引力常数.

2.水的侧压力

设D是与水面垂直的且位于水面之下的平板（见图附2），则D所受到的侧压力为

其中，ρ是水的重度，f（x）为水深x处平板D的宽度，x₁，x₂分别为D中各点坐标的最小者与最大者.

图附 2

【典型例题】

例附2.1 设有一质量为M、长为l的均匀杆AB，一质量为m的质点C位于AB的中垂线上，且与AB的距离为a.

（1）求杆AB对质点C的引力；

（2）当质点C在杆AB的中垂线上从点C移向y轴的正向无穷远处时，为克服引力所做的功有多大？

精解 （1）以AB的中点为原点，杆AB所在的直线为x轴，AB的中垂线为y轴，建立坐标系，如图附2.1所示.在此坐标系下，用引力计算公式计算杆AB对质点C的引力.

图附 2.1

在图附2.1的坐标系下，C=（0，a），在AB上任取一点（x，0），则r=（x-0）i+（0-a）j=xi-aj.其模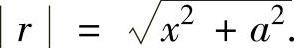杆AB的密度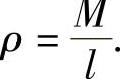于是由引力计算公式可得杆AB对质点C的引力为

（2）由（1）的计算知，当质点C位于点（0，y）（y≥a）时为克服受到AB的引力必须施加力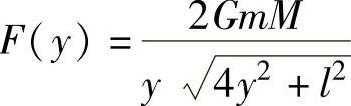，它使质点沿y轴移到+∞处时所做的功

图附 2.2

例附2.2 设一等腰梯形水闸，上底与下底长度分别为a，b（a>b），上底与水面齐平，侧边与水面夹角为α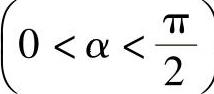（见图附2.2），求此闸门所受的水压力.

精解 建立坐标系如图附2.2所示，利用公式(www.xing528.com)

（其中，ρ为水的重度，h为闸门高度，f（x）为水深x处闸门的宽度）计算闸门所受的压力.由题设知闸门的高度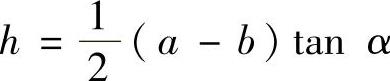，并由图附2.2可见，在水深x处闸门的宽度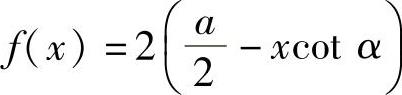，所以闸门所受的水压力

图附 2.3

例附2.3 一铅直倒立的等腰三角形闸门，底边长为a m，高为h m，底边与水面齐平（如图附2.3所示）.

（1）求水闸所受压力；

（2）求水平直线，它将水闸分成所受压力相等的上、下两部分.

精解 （1）建立如图附2.3所示的坐标系，利用公式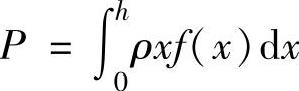（其中ρ是水的重度，f（x）为水深x处闸门的宽度）计算闸门所受的压力.

由图附2.3可知，水深x处闸门的宽度

所以，闸门所受压力为

（2）设所求水平直线距等腰三角形底边b m，则水闸在这条水平线以下部分所有压力P₁为

于是，由题设得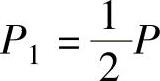，即

即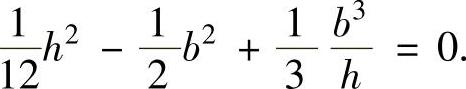

解此方程得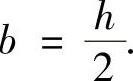

注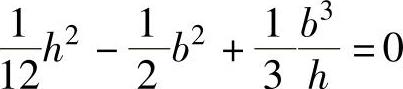具体求解如下：所给方程即为

4b³-6b²h+h³=0，

（4b³-2b²h）-（4b²h-h³）=0，

2b²（2b-h）-h（2b-h）（2b+h）=0，

（2b-h）（2b²-2bh-h²）=0，

由此得到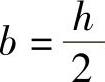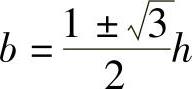，（不合题意，舍去）.