变力做功，计算克服重力所做的功W

【主要内容】

质点M在变力F的作用下沿x轴从点A（其坐标为x₀）移动到点B（其坐标为x₁），则所做的功为

【典型例题】

例附1.1 设半径为R的半球体沉入水中，其大圆所在平面正好与水面齐平，球的重度为ρ（ρ>1）.现将球从水中提出，问做功多少？（假设水的重度为ρ₁，水面的高度不变.）

图附1.1

精解 这是一个变力做功的问题.由于在半球体被提出水面的过程中，在水下部分体积不断减少，即浮力不断减少.因此只要写出球心位于（0，0，t）（0≤t≤R）处时半球体的位于水中的体积V（t）即可.

以xOy平面为水面，球心的初始位置为原点作直角坐标系，如图附1.1所示，当球心位于（0，0，t）时，该半球体排开水的体积为图中阴影部分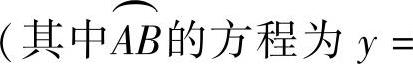 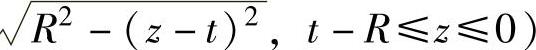绕z轴旋转一周而成的旋转体体积V（t），即

由此可知，半球呈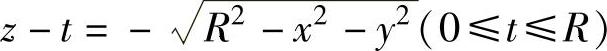状态时，半球的受力为

于是，将半球从水中取出所做的功为

图附 1.2(www.xing528.com)

例附1.2 为了清除井底的污泥，用缆绳将抓斗放入井底，抓起污泥后提出井口（见图附1.2）.已知井深30m，抓斗自重400N，缆绳每米重50N，抓斗抓起的污泥重2000N，提升速度为3m/s，在提升过程中污泥以20N/s的速率从抓斗缝隙中漏掉.现将抓起污泥的抓斗提升至井口，问克服重力所做的功为多少焦耳？（其中1N×1m=1J，m，N，s，J分别表示米、牛顿、秒及焦耳，此外，抓斗高度及位于井口上方的缆绳长度忽略不计）.

精解 克服重力所做的功W是由三部分组成：

W=W₁+W₂+W₃，（1）其中W₁，W₂，W₃分别是克服抓斗自重、缆绳重力及污泥重力所做的功.因此只要分别计算W₁，W₂及W₃即可.

显然W₁=400×30（J）=12000（J）.（2）

下面计算W₂和W_3.

克服缆绳重力的做功是变力沿直线做功问题，其变力为缆绳重力，当缆绳有x m在井中时，其重力为50x，因此

克服污泥重力做功也是变力沿直线做功问题，其变力为污泥的重力.当缆绳有x m在井中时，污泥的重力为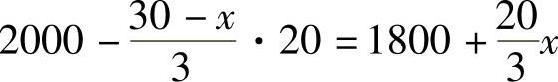，因此

将式（2）～式（4）代入式（1）得

W=12000+22500+57000（J）=91500（J）.