【主要内容】
求满足方程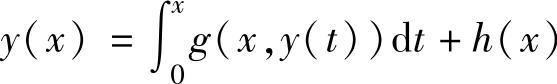 (其中,g(x,u)是已知的连续函数,h(x)是已知的可微函数)的连续函数y(t)的步骤如下:
(其中,g(x,u)是已知的连续函数,h(x)是已知的可微函数)的连续函数y(t)的步骤如下:
(1)将g(x,y(t))中的x移走,例如移出到积分号外,或通过适当的变量代换移到积分上限.
(2)经过上述处理后的方程两边对x求导(一次或两次)转换成微分方程,求解此微分方程(此时的初始条件可从所给的方程中得到), 即得未知函数y(x)的表达式.
【典型例题】
例4.7.1 求满足方程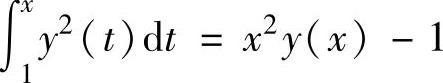 的连续函数y(x)(x≥1).
的连续函数y(x)(x≥1).
精解 由y(x)连续知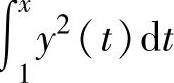 可导,从而由所给方程知y(x)(x≥1)可导.因此,所给方程两边对x求导得
可导,从而由所给方程知y(x)(x≥1)可导.因此,所给方程两边对x求导得
y2(x)=2xy(x)+x2y′(x),
即
令y=xu,代入式(1)得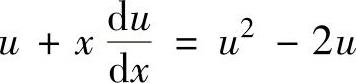 ,即
,即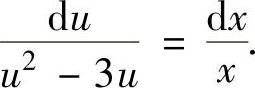
上式两边分别积分得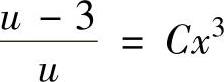 ,即
,即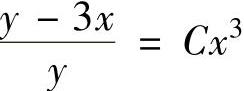 .由此得到
.由此得到
由所给的方程知y(1)=1.将它代入式(2)得得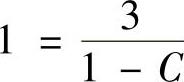 ,即C=-2.将它代入式(2)
,即C=-2.将它代入式(2)
例4.7.2 设φ(x)是连续函数,且满足方程
求φ(x).
精解 将所给方程改写成
(即将被积函数中的x移出积分号),并在上式两边对x求导(由于φ(x)连续,所以由上列表达式知φ(x)可导)得
即
式(1)两边对x求导得φ″(x)=ex-φ(x),即 φ″(x)+φ(x)=ex.(2)
它有特解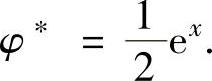 此外它对应齐次线性微分方程φ″(x)+φ(x)=0的通解为Φ=C1 sin x+C2 cos x.因此式(2)的通解为
此外它对应齐次线性微分方程φ″(x)+φ(x)=0的通解为Φ=C1 sin x+C2 cos x.因此式(2)的通解为
并且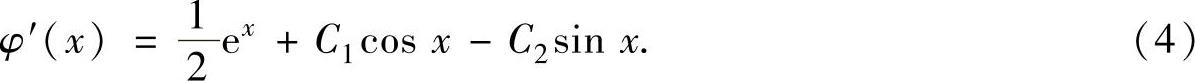
由题设中所给的方程及式(1)知φ(0)=1,φ′(0)=1.将它们代入式(3)和式(4)得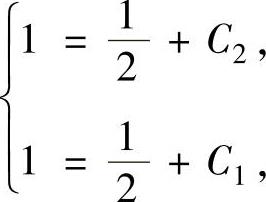 即
即 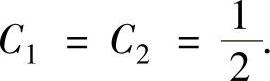
将它们代入式(3)得
例4.7.3 设函数y(x)具有连续导数,且满足方程
及y(0)=1,求y(x)的表达式.
精解 首先应由变量代换u=xt将∫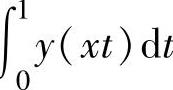 中的x移到积分上限:
中的x移到积分上限:
将它代入所给方程得(https://www.xing528.com)
上式两边对x求导得
y″+3y′+2y=e-x(二阶常系数非齐次线性微分方程),(1)
式(1)对应的齐次线性微分方程为
y″+3y′+2y=0,(2)
它的特征方程r2+3r+2=0有根r=-1,-2,所以式(2)的通解为
Y=C1 e-x+C2 e-2x.
此外,式(1)有特解y∗=Axe-x.将它代入式(1)得
(Axe-x)″+3(Axe-x)′+2(Axe-x)=e-x,
即A(x-2)e-x+3A(1-x)e-x+2Axe-x=e-x.
化简得A=1,所以式(1)有特解y∗=xe-x.从而式(1)的通解为y(x)=C1 e-x+C2 e-2x+xe-x,(3)
且y′(x)=-C1 e-x-2C2 e-2x+(1-x)e-x.(4)由题设知y(0)=1,此外由所给方程知y′(0)=-1,将它们代入式(3)、式(4)得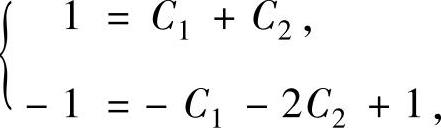
即C1=0, C2=1.
将它们代入式(3)得所求的
y(x)=e-2x+xe-x.
例4.7.4 设连续函数y(x)满足方程
且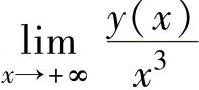 存在,求y(x)的表达式.
存在,求y(x)的表达式.
精解 将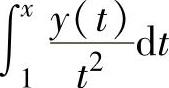 前的x除去得
前的x除去得
上式两边分别对x求导得
化简后得
令p=y′,则式(1)成为
它的通解为
于是式(1)的通解为
下面确定式(2)中的C1与C2.由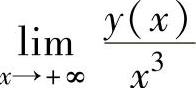 存在知C1=0,所以
存在知C1=0,所以
将x=1代入所给的方程得y(1)=1+y′(1).于是由式(3)得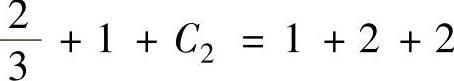 ,即
,即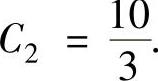
将它代入式(3)得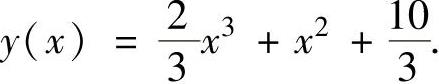
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




