2015考研数学-曲线弧长与旋转曲面侧面积计算

【主要内容】

1.曲线弧长的计算设曲线弧的参数方程为{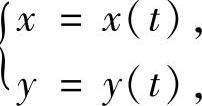其中A，B的参数分别为α，β（α<β），x（t），y（t）都是连续可导函数，则的弧长为

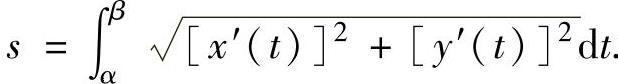
特别地，曲线弧的方程为y=f（x），A，B的横坐标分别为x₀，x₁（x₀<x₁），f（x）连续可导，则的弧长为

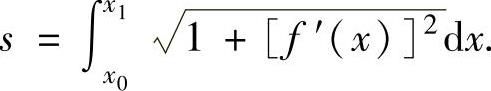
设曲线弧的极坐标方程为r=r（θ），设A，B的极角分别为θ₀，θ₁（θ₀<θ₁），r（θ）连续可导，则的弧长为

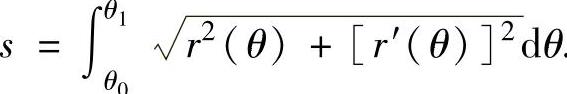
2．旋转曲面侧面积的计算

(1)设帆线弧y=f(x)（a≤x≤6）（其中，函数f(x)在[a，b]上连续可导），则它绕戈轴旋转一周而成的旋转曲面侧面积为

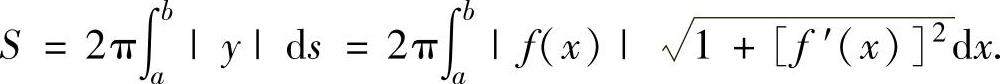
注 此时旋转曲面方程为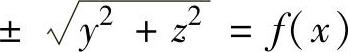，即y²+z²=f²（x）.

（2）设曲线弧x=g（y）（c≤y≤d）（其中，函数g（y）在[c，d]上连续可导），则它绕y轴旋转一周而成的旋转曲面侧面积为

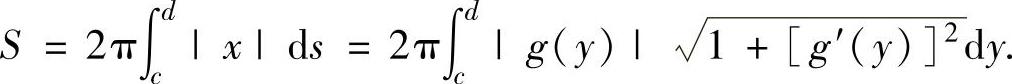
注 此时旋转曲面方程为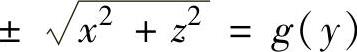，即x²+z²=g²（y）.

【典型例题】

例2.14.1 在曲线弧A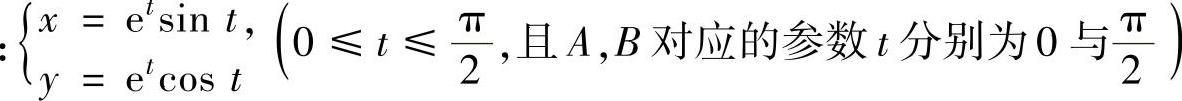上求一点C，使的弧长为弧长的2倍.

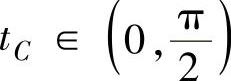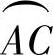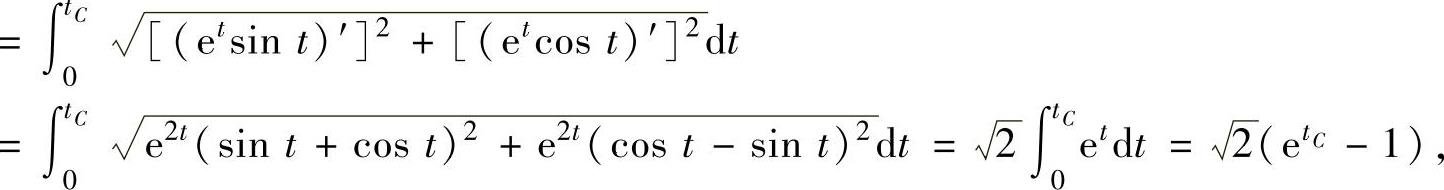
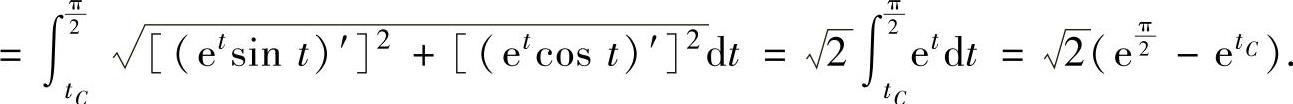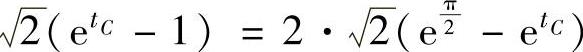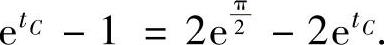精解 设点C对应的参数为，则的弧长的弧长所以，由题设得，即解此方程得

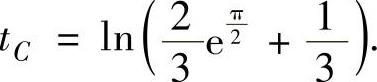
因此C点的坐标为，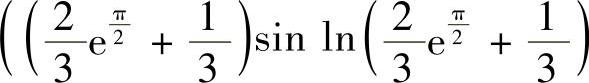

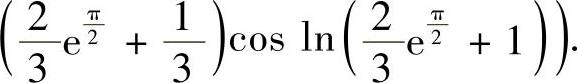
例2.14.2 设s（φ）表示对数螺线r=e^aθ（a>0）自θ=0到θ=φ（φ>0）的弧长，A（φ）表示由这段曲线与射线θ=0，θ=φ围成的曲边扇形的面积，求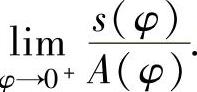

精解 先算出s（φ）和A（φ），然后计算所给的极限.由于

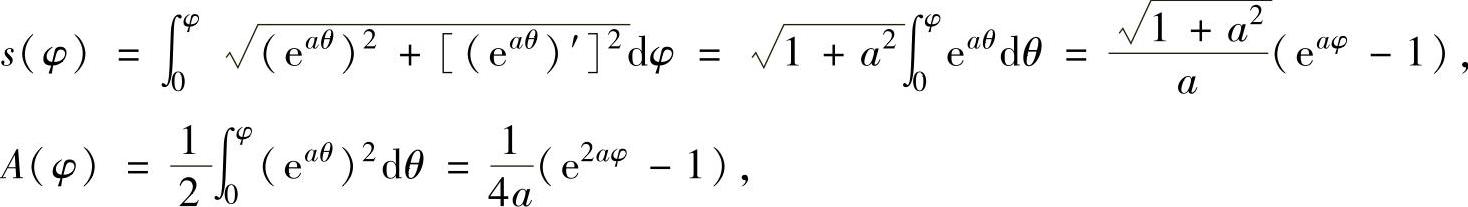
所以，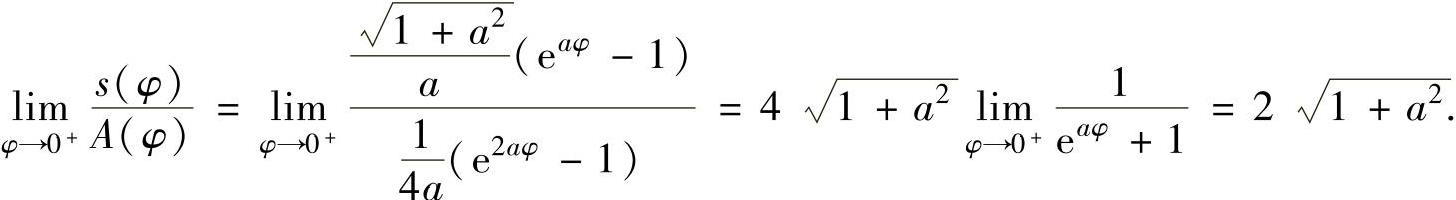

例2.14.3 设ρ=ρ（x）是抛物线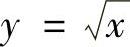上任一点M（x，y）（x≥1）处的曲率半径，s=s（x）是该抛物线上介于点A（1，1）与点M之间曲线弧的弧长，求(https://www.xing528.com)

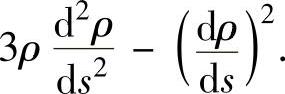
精解 由抛物线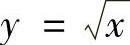 在点M（x，y）的曲率为

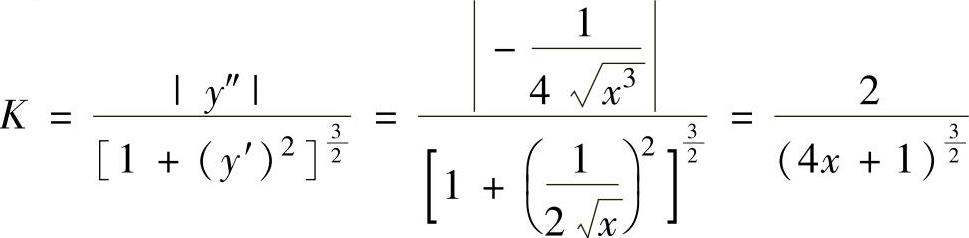
知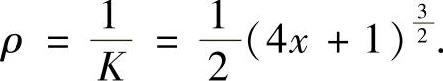，此外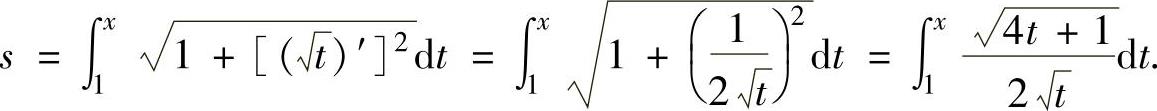，由此得到由参数方程 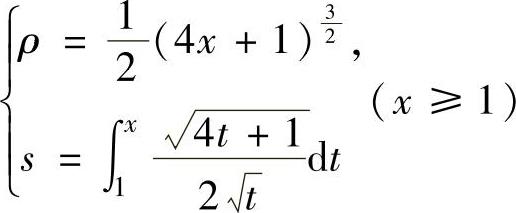表示的函数ρ=ρ（s），由参数方程表示的函数求导方法得

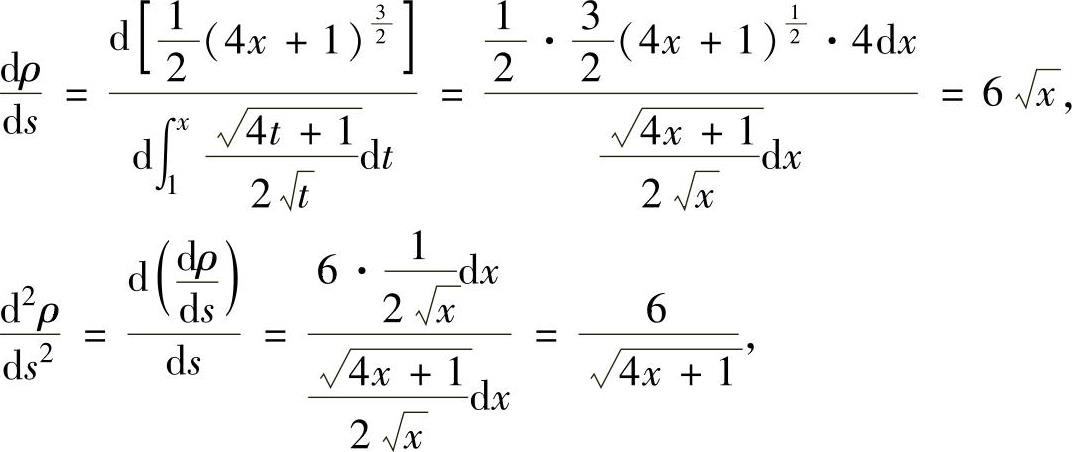
所以，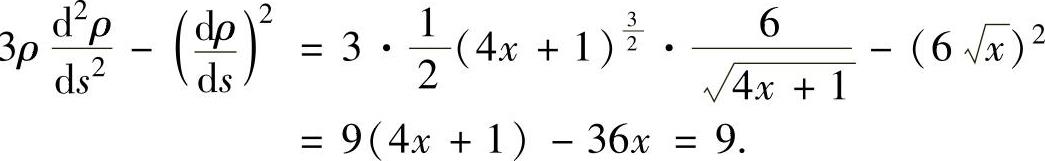

例2.14.4 设曲线C：y=x²，记A（t）是由曲线C，直线x=-1，x=t（t>-1）及x轴围成的曲边梯形的面积，s（t）为曲线C上从点（-1，1）到（t，t²）的曲线弧的弧长.现将由参数方程表示的曲线C₁：

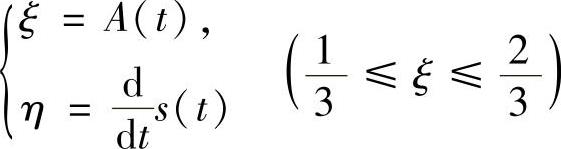
绕ξ轴旋转一周，求由此产生的旋转曲面的侧面积S.

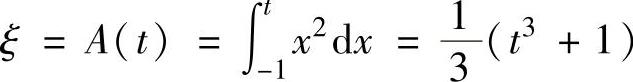精解 先确定A（t），的表达式，然后求旋转曲面的侧面积S.，由此可得当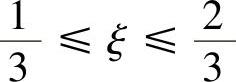时，0≤t≤1.此外由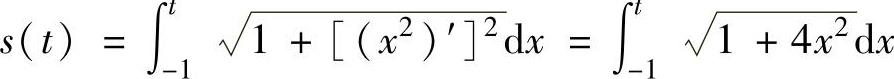得

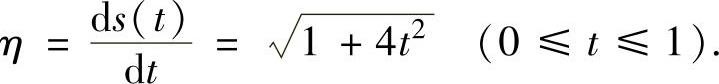
所以，所求的旋转曲面的侧面积

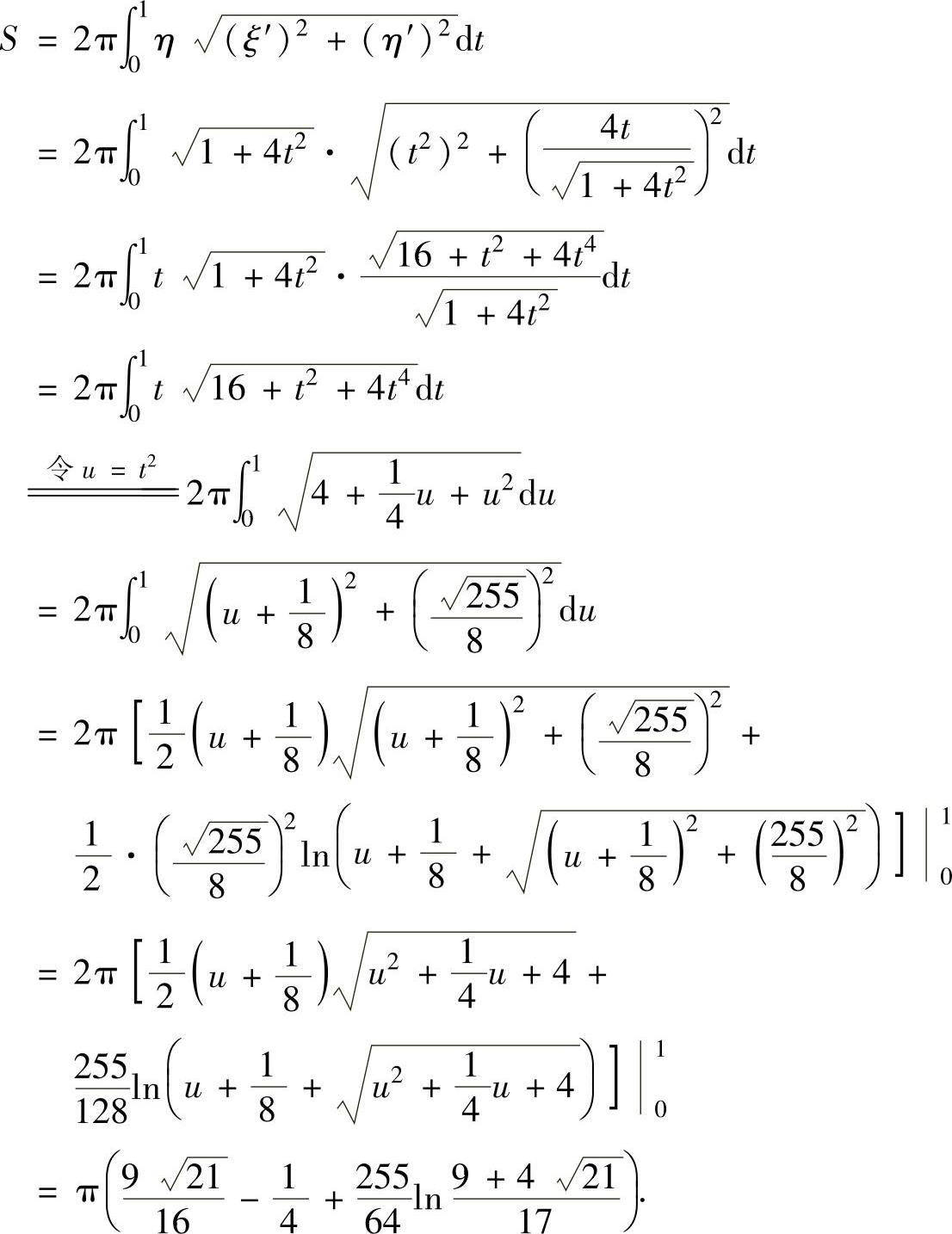
例2.14.5 设有曲线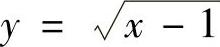，过原点作其切线，求由此曲线、切线及x轴围成的平面图形D绕x轴旋转一周而成的旋转体表面积S.

精解 先计算切线方程并画出D的图形，然后按旋转体侧面积计算公式计算S.

切线方程应为y=kx.设切点为（x₀，y₀），则k，x₀，y₀满足方程组

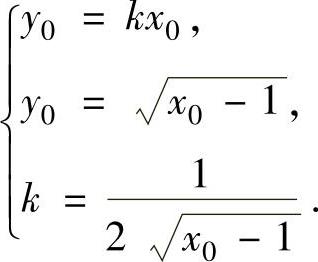
解此方程组得x₀=2，y₀=1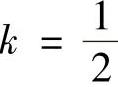，，所以切线方程为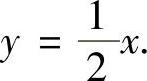由此可画出D的图形如图2.14.5阴影部分所示.由图可知

S=S₁+S₂，其中，S₁是由 绕x轴旋转一周而成的旋转曲面面积，S₂是由曲线弧绕x轴旋转一周而成的旋转曲面面积.所以

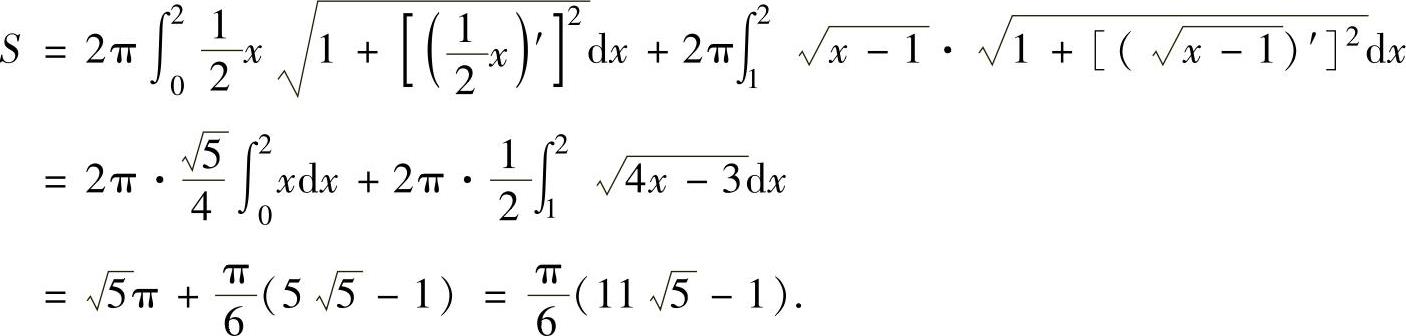
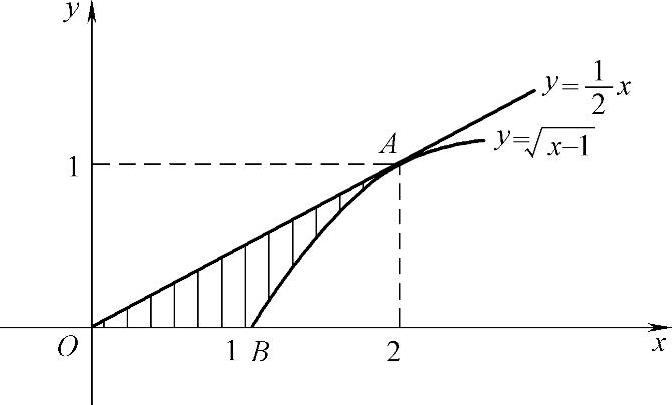
图 2.14.5