曲线凹凸性、拐点的计算及曲率、曲率圆

1.曲线凹凸性及其判定方法

在某个区间内，如果曲线位于其上任意一点的切线的上方（下方），则称曲线在该区间内为凹的（凸的）.

曲线y=f（x）在区间I上凹凸性的判定方法是：

设函数f（x）在I上二阶可导.如果f″（x）>0（x∈I），则曲线y=f（x）在I上是凹的；如果f″（x）<0（x∈I），则曲线y=f（x）在I上是凸的.

2.曲线拐点及其计算方法

设函数f（x）连续，则曲线y=f（x）上的凹弧与凸弧的分界点称为该曲线的拐点.

曲线y=f（x）（f（x）是连续函数）的拐点可按以下步骤计算：

（1）在f（x）的定义域上，求方程f″（x）=0的实根和使f″（x）不存在的点，设为x₁，x₂，…，xn；

（2）对由步骤（1）算得的每个x_i，如果在其两侧邻近f″（x）为异号，则（x_i，f（x_i））是曲线y=f（x）的一个拐点，否则点（x_i，f（x_i））不是曲线y=f（x）的拐点.

3.曲率与曲率圆的概念

这里，考察的曲线y=f（x）是光滑的（即该曲线的每一点都有切线）.

如果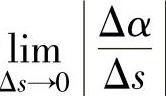（其中，Δs为曲线y=f（x）的

（的长度，Δα为动点M′沿M移动到点M时相应的切线转过的角度）存在，则称这个极限值K为曲线y=f（x）在点M处的曲率，即

如果函数f（x）二阶可导，则

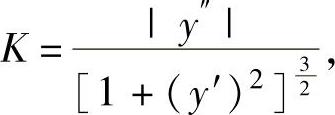
并称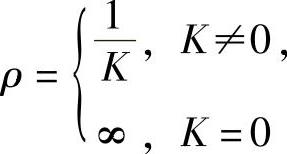为曲线y=f（x）在点M处的曲率半径；当K≠0时，以点D为中心、ρ为半径的圆称为曲线y=f（x）在点M的曲率圆，其中D是在点M处的曲线的法线上，且在凹的一侧所取的点，它与点M的距离为ρ.所以，曲率圆与曲线在点M处有相同的切线和曲率，且在点M处有相同的凹凸性.

【典型例题】

例1.22.1 计算下列曲线y=f（x）的凹凸区间（即曲线y=f（x）凹弧区间与凸弧区间）与拐点：

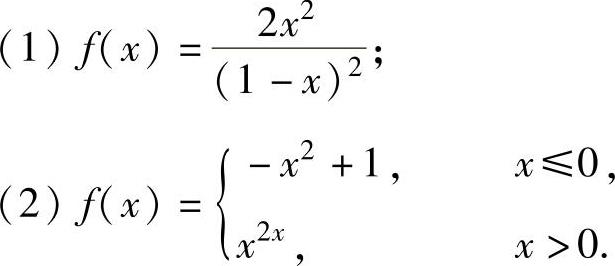
精解 （1）y=f（x）的定义域为（-∞，1）∪（1，+∞），且在其上二阶可导，

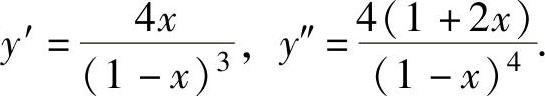
显然使y″=0的点为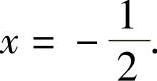据此列表如下：

由表可知，曲线y=f（x）的凸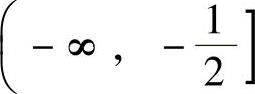区间为，凹区间为和（1，+∞），拐点为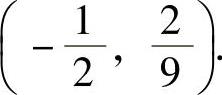

（2）y=f（x）的定义域为（-∞，+∞），且在其上连续，此外有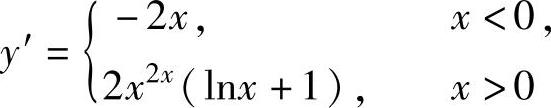（这里不必确定y在点x=0处的可导性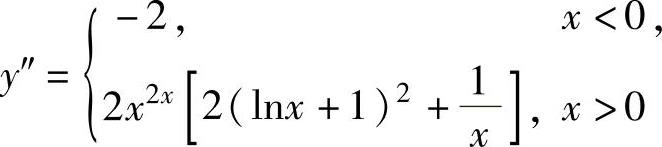），（这里不必确定y′在点x=0处的可导性），由此可知，曲线y=f（x）（连续函数）的凸区间为（-∞，0]，凹区间为[0，+∞），拐点为（0，1）.

例1.22.2 （单项选择题）曲线y=（x-1）（x-2）2（x-3）3（x-4）4的拐点是（ ）.

A.（1，0） B.（2，0） C.（3，0） D.（4，0）

精解 由

可得y=（x-1）（x-2）2（x-3）3（x-4）4的概图如图1.22.2所示.由图可知点（3，0）是所给曲线的拐点.

因此本题选C.

图 1.22.2(www.xing528.com)

例1.22.3 （单项选择题）设函数f（x）满足f（x）=-f（-x），x∈（-∞，+∞），且在（0，+∞）上f′（x）>0，f″（x）>0，则f（x）在（-∞，0）上（ ）.

A.单调增加且其图形是凹的

B.单调增加且其图形是凸的

C.单调减少且其图形是凹的

D.单调减少且其图形是凸的

精解 由f（x）是奇函数知f′（x）是偶函数，f″（x）是奇函数，所以在（-∞，0）上f′（x）>0，f″（x）<0，即在（-∞，0）上f（x）单调增加且其图形是凸的.

因此本题选B.

例1.22.4 计算下列各题：

（1）求曲线y=lnx上曲率K（x）最大的点；

（2）求曲线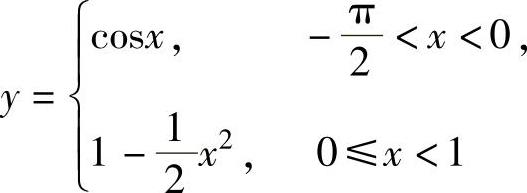的曲率K（x）.

精解 （1）先算出曲率K（x），然后计算使它取得最大值的x.y=lnx的定义域为（0，+∞），在其定义域内

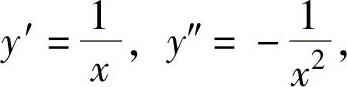
所以显然K（x）在（0，+∞）上可导且

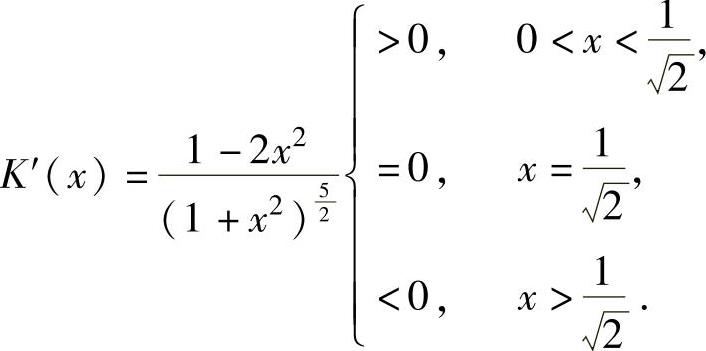
由此可知，K（x）在点处取得最大值，即曲线y=lnx的最大曲率点为

（2）先算出y′，y″，然后按曲率公式计算所给曲线的曲率.当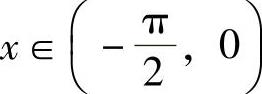时，y′=-sin x；当x∈（0，1）时，y′=-x，并且由

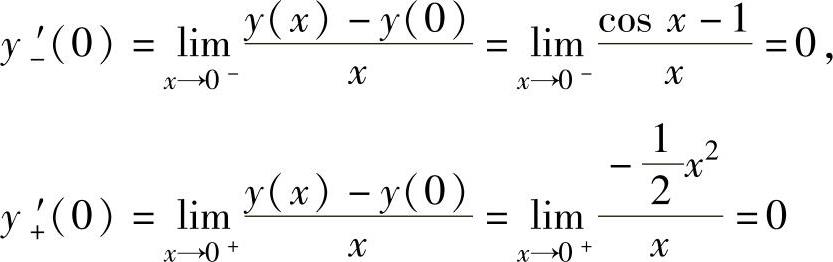
知y′（0）=0.于是有

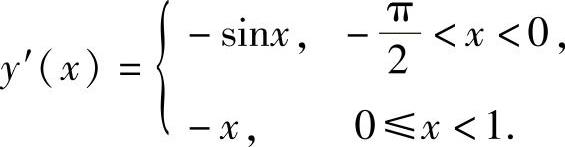
此外，当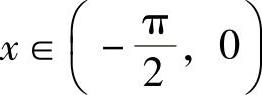时，y″=-cos x；当x∈（0，1）时，y″=-1，并且由

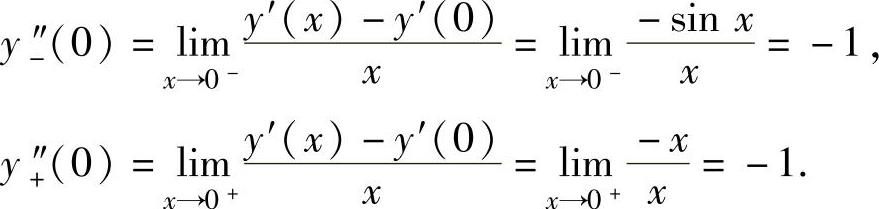
知y″（0）=-1.于是有

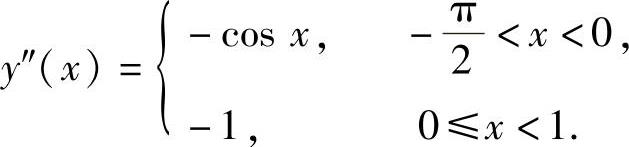
由此可得

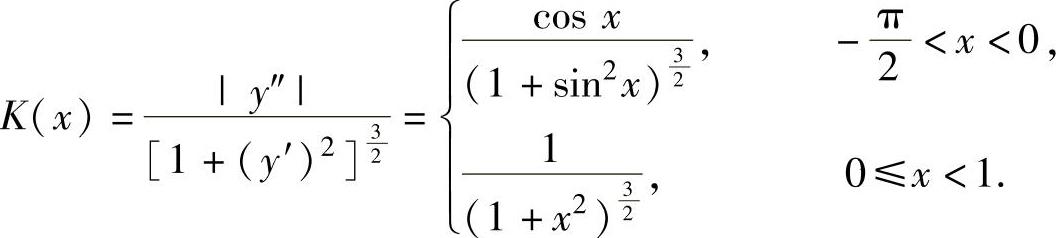
例1.22.5 （单项选择题）设f″（x）不变号，且曲线y=f（x）在点（1，1）处的曲率圆为x²+y²=2，则函数f（x）在（1，2）内（ ）.

A.有极值点，无零点 B.无极值点，有零点

C.有极值点，有零点D.无极值点，无零点

精解 由于曲线y=f（x）与曲率圆x²+y²=2在点（1，1）处有相同的切线，从而

f′（1）=y′（1）=-1（曲率圆x²+y²=2在点（1，1）的切线斜率为-1）.（1）此外，曲线y=f（x）与x²+y²=2在点（1，1）邻近有相同的凹凸性，而x²+y²=2在点（1，1）邻近是凸的，从而f″（1）<0.由于f″（x）不变号，所以在（1，2）内f″（x）<0，即f′（x）单调减少，故f′（x）<f′（1）=-1<0，x∈（1，2），从而f（x）在（1，2）内无极值点.

最后，由f（1）=1，f（2）=f（1）+[f（2）-f（1）]=1+f′（ξ）<1+f′（1）=0（其中ξ∈（1，2））知，f（1）f（2）<0，从而由连续函数零点定理得f（x）在（1，2）内有零点.

因此本题选B.