总体X为概率论与数理统计学习指导书中的研究对象

1.总体、个体、样本、样品与简单随机样本是什么？

答　研究对象的全体称为总体，记为X；组成总体的每个基本单位称为个体，记为X1，X2，…，Xn，….在总体X中随机地抽取的n个个体X1，X2，…，Xn称为总体X的样本.组成样本的个体称为样品.由简单随机抽样得到的样本称为简单随机样本.

2.简单随机样本的性质是什么？

答　性质1：X1，X2，…，Xn具有代表性，即具有随机性.

性质2：X1，X2，…，Xn具有独立同分布性.

有放回地随机抽取得到的是简单随机样本，一般如果样本容量相当大，随机抽取的样本对于总体容量来说是很小的，也认为是有关简单随机样本.

3.说明样本均值与样本方差及其应用.

答　设总体X的容量为n的样本为X1，X2，…，Xn，称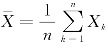为样本均值；称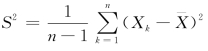为样本方差；当总体均值μ和总体方差σ2未知时，用样本均值作为总体均值的估计值；用样本方差作为总体方差的估计值，即E=μ，ES2=σ2称为点估计.

4.统计量是什么？(www.xing528.com)

答　设X1，X2，…，Xn是总体X的样本，令φ（X1，X2，…，Xn）为定义在样本X1，X2，…，Xn上的函数，若函数中不包含任何未知参数，则称φ（X1，X2，…，Xn）为一个统计量，统计量为随机变量函数.

5.写出三个来自正态总体的样本所构成的常用统计量的分布.

答　设总体X～N（μ，σ2），X1，X2，…，Xn是总体X的一个样本，则

（1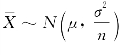），其标准化的随机变量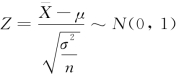为一个统计量，且满足

或

（2）设样本均值，样本方差S2，则统计量为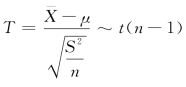，且满足

（3）统计量，且满足