离散型随机变量概述及分布律特点与性质

1.随机变量及其分类是什么？

答　在随机试验中，依赖试验结果的不同取不同值的量为随机变量.按照随机变量的取值规律，可分为离散型（变量取值为有限个或可数无穷多个数值）和连续型（变量可取某一区间内的任何值）.

2.离散型随机变量分布律的表示法是什么？

答　设随机变量X的可取值为x1，x2，…，xn，X在这些值的概率依次为p1，p2，…，pn，则分布律有

（1）公式法P（X=xk）=pk，k=1，2，…，n；

（2）图示法（略）；

（3）列表法（见下表）.

3.离散型随机变量分布律的性质有哪些？

答　（1）非负性：pk≥0，k=1，2，…，n；

（2）归一性：.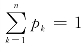

4.常用的离散型随机变量的分布有哪些？

（1）（0-1）分布：试验只有两个互斥的结果A与，便可定义一个函数其分布律为

P（X=k）=pkq1-k，k=0，1.

（2）二项分布：在一次试验中事件A发生的概率为p（0＜p＜1），在n次重复独立试验中A发生k次的概率为二项分布

记为X～B（n，p）.

（3）超几何分布：这是计件抽样检验中一个重要的计算公式，它全面地表示了无放回抽取中取得次品数X取值的概率分布为

（4）泊松分布：这种分布常应用稠密问题，如候车的人数、原子放射粒子数等.X取值的概率分布为

记为X～π（λ）.

泊松分布与二项分布存在着某种联系，当n充分大时，令λ=np，

5.分布函数及其分类是什么？

答　设X为随机变量，x为任意实数，称F（x）=P（X≤x）为X的分布函数.

对于任意实数x，有

6.分布函数的性质有哪些？

答　（1）单调不减性：若x1＜x2，则F（x1）≤F（x2）；

（2）右连续性：F（x+）=F（x）；

（3）归一性：对任意实数.

7.连续型随机变量的概率密度是什么？

答　对于随机变量X，若存在一个定义在（-∞，+∞）内的非负函数f（x），使得成立，则称X为连续型随机变量，称f（x）为X的概率密度函数.同时，对任意的a，b有成立.

8.密度函数有哪些性质？

答　（1）；（2）P（X=k）=0.

这个性质使得

9.写出常用的连续型随机变量X的密度函数和分布函数.(www.xing528.com)

答　（1）均匀分布：X的一切可能值充满着某一区间（a，b），其概率密度函数为

其分布函数为

X服从参数为a，b的均匀分布，记为X～U（a，b）；

（2）指数分布：X的密度函数为

其分布函数为

X服从参数为λ的指数分布，记为X～E（λ）.

（3）正态分布：X的密度函数为

其分布函数为

X服从参数为μ，σ2的正态分布，记为X～N（μ，σ2）.

（4）标准正态分布：X的密度函数为

记为X～N（0，1）.

其分布函数为

两个重要的概率积分公式:.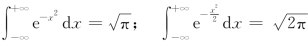

10.写出利用正态分布表计算概率的公式.

答　当X～N（0，1）时，

（1）Φ（0）=0.5；Φ（-x）=1-Φ（x）；P（|X|≤a）=2Φ（a）-1.

（2）P（a＜X＜b）=Φ（b）-Φ（a）；

P（X＜b）=P（X≤b）=Φ（b）；

P（X≥a）=P（X＞a）=1-P（X≤a）=1-Φ（a）.

11.写出一般正态分布的概率计算

答　当X～N（μ，σ2）时，令，则

即

12.随机变量的函数及其概率分布是什么？

答　X为随机变量，则函数Y=g（X）也是随机变量，每当X取x时，Y随之取值g（x）.

离散型随机变量X的分布律：

离散型随机变量X的函数Y=g（X）的分布律：

连续型随机变量X的函数Y=g（X）的概率分布：

设X的密度函数为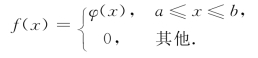

设Y=g（X），y=g（x）必须单值单调可导的密度函数为

其中是Y=g（X）的反函数.