计算的执行顺序会影响目标代码的效率。之前,是按照基本块中间代码序列的顺序,依次生成其目标代码的。这么做尽管很简单,但是生成的代码未必高效。为了解决这个问题,需要使用中间代码的DAG图,重新对其结点进行排序,以改变计算的执行顺序。下面通过一个例子来说明。
例9.6 某基本块的中间代码序列如下:
T1:=A+B
T2:=C+D
T3:=E-T2
T4:=T1-T3
假设R0和R1为可用的寄存器,T4是基本块出口之后的活跃变量,于是,利用简单代码生成算法可以生成如下的目标代码:
MOV R0,A
ADD R0,B
MOV R1,C
ADD R1,D
MOV T1,R0
MOV R0,E
SUB R0,Rl
MOV R1,T1
SUB R1,R0
MOV T4,R1
画出该中间代码序列的DAG,如图9-3所示。
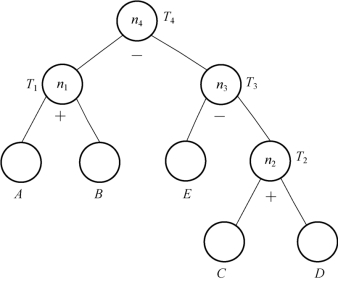
图9-3 中间代码序列的DAG
利用图9-3的DAG,可将该中间代码序列改写为:
T2:=C+D(https://www.xing528.com)
T3:=E-T2
T1:=A+B
T4:=T1-T3
这和改写前的中间代码逻辑上是等价的。同样,应用简单代码生成算法可生成如下的目标代码:
MOV R0,C
ADD R0,D
MOV R1,E
SUB R1,R0
MOV R0,A
ADD R0,B
SUB R0,R1
MOV T4,R0
与前者生成的目标代码相比,后者减少了两条指令,从而提高了执行效率。此例说明,代码执行的次序会直接影响执行的效率。使得例9.6中代码效率提高的原因是计算完T1的值后,及时利用T1在寄存器中的值来计算T4,而不是把T1的值先存放到内存单元中,待计算T4时,再把T1的值由内存单元取到寄存器中,从而减少了寄存器回写内存单元以及从内存单元中取值到寄存器的代码。
当计算一个表达式的值时,各操作数可以有不同的结合次序,既可以从左到右,也可以从右到左。从右到左计算使得每一个被计算的量,总是紧接在其左运算对象之后计算,从而充分利用寄存器。例9.6的中间代码序列对应于赋值句T4:=A+B-(E-(C+D)),后者所生成的目标代码执行效率的提高正是赋值句右部表达式从右到左计算的结果。
按照上述思路,可以利用基本块的DAG给基本块的中间代码序列重新排序,尽可能地使一个结点的求值紧接在它的最左运算对象的求值之后,以提高目标代码的效率。
算法9.4 给DAG中的结点重新排序。

最后,T[l],T[2],…,T[N]即为所求的结点顺序。
按照算法9.4得到的结点次序,可以生成新的中间代码序列,其逻辑上是等价的。利用新的中间代码序列,就能够生成效率较高的目标代码。
在算法9.4中,计算叶结点值的中间代码无须生成。计算内部结点值时若要引用叶节点的值,则直接引用其标记即可。叶节点上附有其他标识符时,生成对标识符的赋值指令的次序并不重要。对例9.6的DAG应用上述算法,可得到各内部结点的次序为n2、n3、n1、n4。正是按这一结点次序生成了新的中间代码序列,进而提高了目标代码的执行效率。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




