编译原理与实践：对折查找和二叉树

为了提高线性表的查表效率，可以把表中所有的项按照名字值的大小顺序重新整理排列，可以规定值小者在前，值大者在后。按照这种思路，图7-5可以改造成图7-6所示的形式。

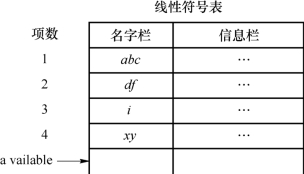
图7-6　线性表

此时，对于这种经过顺序化整理了的符号表的查找可以采用对折法。所谓对折查找法是指，假定符号表中含有n个表项，若要查找某项sym时，需要：

（1）首先把sym和中项（即第[n/2]+1项）做比较，若相等，则宣布查到；

（2）若sym小于中项，则继续在1～[n/2]的各项中去查找；

（3）若sym大于中项，则就到[n/2]+2～n的各项中去查找。(www.xing528.com)

这样做的好处是，经一次比较就可以排除n/2项。当继续在1～[n/2]或[n/2]～n的范围中查找时，同样采取上述（1）～（3）的办法，若还找不到，则再把查找范围折半。显然，使用对折法每查找一项最多只需作1+log2 N次比较，因此，也可将该方法称作对数查找法。

虽然这种方法很好，但是对于一遍扫描的编译程序来说用处不大，这是因为符号表一般是边填边引用的，若每填入一个新项都得做顺序化的整理工作，势必造成时间的极度浪费。因此，通常的做法是，将符号表组织成一棵二叉树，令每项作为一个结点，结点的主栏内码值被看成是代表该结点的值，并且，给每个结点附设2个指示器栏，一栏为left（左枝），另一栏为right（右枝）。对于这种二叉树，要求任何结点p右枝的所有结点值均应小于结点p的值，而左枝的任何结点值均应大于结点p的值。

二叉树的构造过程可以描述为：令第一个碰到的名字为“根”结点，其左、右指示器均置为null。当加入新结点时，先把它和根结点的值做比较，小者放在右枝上，大者放在左枝上。如果根结点的左（右）枝已成子树，则让新结点和子树的根再作比较。重复上述操作，直至该新结点成为二叉树的一个端末结点（叶）为止。按照这一过程，可将图7-5的线性表表示为如图7-7所示的二叉树。

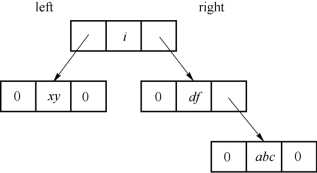
图7-7　线性表的二叉树表示

显然，二叉树的查找效率比对折查找效率稍低一点，而且由于增加了左、右指示器，存储空间也得多耗费一些。但是，它所需要的顺序化时间却大大减少，而且每查找一项所需的比较次数仍然与log2 N成比例，因此，它已成为实际应用中不可缺少的一种符号表查找方法。