LALR(1)分析的应用与实践

在LR（1）分析表中，若存在两个状态（项目集）除向前搜索符不同外，其他部分都是相同的，则称这样的两个LR（1）项目集是同心的，相同部分称为同心项目集的心。例如，图5-9中的I3和I6是同心的。如果将同心的LR（1）项目集合并，心仍为相同的一个LR（0）项目集。超前搜索符集是各同心集超前搜索符的并集，合并同心集后GOTO函数自动合并。例如，将I3和I6合并后得到

I36:{[B→b·B,a/b/#],[B→·bB,a/b/#],[B→·a,a/b/#]}

其中，[B→b·B，a/b/#]是[B→b·B，a]、[B→b·B，b]和[B→b·B，#]三个项目的简化表示。若合并LR（1）项目集规范族中的同心集后没有产生新的冲突，称为LALR（1）项目集。

这种LR分析法称为LALR方法，即向前LR分析。LALR的功能和代价介于SLR和规范LR之间，可用于大多数程序设计语言的文法，并可高效地实现。对同一个文法来说，LALR分析表和LR（0）、SLR分析表具有相同数目的状态。LALR分析表比LR（1）分析表小得多，能力也弱一些，但能够应用于一些SLR（1）不能应用的情况。文法的描述能力可以形象地表示为

LR（0）⊂SLR（1）⊂LR（1）⊂LALR（1）⊂无二义文法

构造LALR分析表的基本思想是首先构造LR（1）项目集族；如果不存在冲突，就将同心集合并；如果合并后的项目集族不存在归约-归约冲突，即不存在同一个项目集中有两个形如A→c·和B→c·的产生式具有相同的搜索符，则按这个项目集族构造分析表。合并同心集可能会推迟发现错误的时间，但错误出现的位置仍是准确的。构造LALR分析表的方法如算法5.9所示。

算法5.9 构造LALR分析表。

（1）构造文法G的LR（1）项目集规范族，C={I0，I1，…，In}。

（2）合并所有的同心集，得到LALR（1）的项目集族C={J0，J1，…，Jm}。含有项目[S→·S，#]的Jk为分析表的初态。

（3）由C构造ACTION表，方法与LR（1）分析表的构造相同。

①若[A→α·aβ，b]∈Jk，且GOTO（Jk，a）=Jj，其中a∈VT，则置ACTION[k，a]=Sj，即将输入符号a和状态j分别移入文法符号栈和状态栈。

②若项目[A→α·，a]∈Jk，其中a∈VT，则置ACTION[k，a]=rj，rj的含义是按产生式A→α进行归约，A→α是文法的第j个产生式。

③若项目[S→S·，#]∈Ik，则置ACTION[k，#]=acc，表示分析成功，接受。

（4）构造GOTO表。对于不是同心集的项目集，GOTO表的构造与LR（1）的相同；对同心集中的项目集，各个项目集经过转换函数后的项目集如果仍为同心集，则GOTO表的构造也相同。(www.xing528.com)

假定Ii1，Ii2，…，Iin是同心集，合并后的新集为Jk，转换函数GOTO（Ii1，X）、GOTO（Ii2，X）、…、GOTO（Iin，X）也为同心集，将其合并后记作Ji，因此，有GOTO（Jk，X）=Ji，所以当X为非终结符时，GOTO（Jk，X）=Ji，则置GOTO（k，X）=i，表示在k状态下遇到非终结符X时，将X和i分别移到文法符号栈和状态栈。

（5）分析表中凡不能在步骤（3）和步骤（4）填入信息的空白处均填上“出错标志”。

依据算法5.9构造的分析表若不存在冲突，则称其为文法G的LALR分析表，能够构造LALR分析表的文法称为LALR文法，使用LALR分析表的分析器称为LALR分析器。

LALR与LR（1）的不同之处在于，当输入串有误时，LR（1）能够及时发现错误，而LALR则可能还继续执行一些多余的归约动作，但决不会执行新的移进，即LALR能够像LR（1）那样准确地指出错误发生的位置。

例5.18 求例5.17中文法的LALR（1）分析表。

根据图5-9的LR（1）项目集规范族，可发现如下的同心集：

将同心集合并后可得

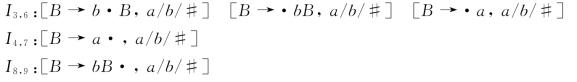
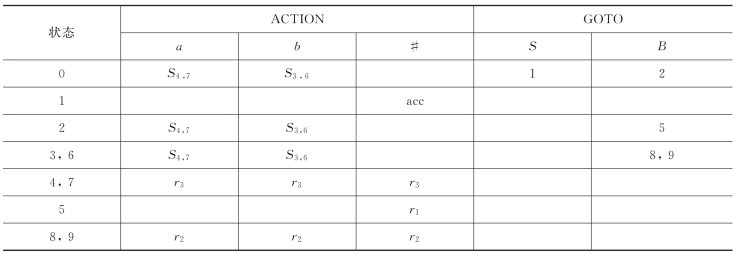
同心集合并后仍不包含冲突，因此，文法是LALR文法。对文法合并同心集后，可构造出如表5-15所示的LALR（1）分析表，该表与文法的LR（0）分析表是相同的。

表5-15　例5.17文法的LALR（1）分析表