编译原理与实践中的优先函数表示终结符的优先关系

利用优先关系表来表示每对终结符之间的优先关系存储量大、查找费时。实际应用中，一般不直接使用优先关系表。如果能够给每个终结符赋一个值，即定义终结符的一个函数f，值的大小反映其优先级别，那么终结符对a、b之间的优先关系就转换为两个优先函数f（a）与f（b）的值的比较。利用优先函数表示终结符之间的优先关系既便于做比较运算，又能节省存储空间。

注意，一个终结符在栈中（左）与在输入串中（右）的优先值是不同的。例如，既存在着+），又存在着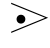）+。因此，一个终结符a应该具有一个左优先数f（a）和一个右优先数g（a）这样一对函数。根据一个文法的算符优先关系表，将每个终结符θ与两个自然数f（θ）和g（θ）对应，如果f（θ）和g（θ）的选择满足如下关系：

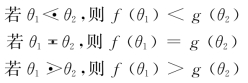
则称f和g为优先函数。其中，f称为入栈优先函数，g称为比较优先函数。注意，由于优先函数与自然数对应，对给定的文法，如果存在优先函数，一定存在多个，即f和g的选择不是唯一的。

1.关系图法

根据优先关系表构造优先函数f和g的一个简单方法是关系图法。关系图是一张有向图，其构造过程如下：

（1）对所有终结符a（包括#）以fa、ga为结点名，画出全部n个终结符所对应的2n个结点；

（2）若ab或a b则画一条从fa到gb的箭弧；若a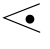b或a b则画一条从gb到fa的箭弧；

（3）如果用上述方法构造的图中存在环路，则不存在优先函数。存在优先函数时，对每个结点都赋予一个数，此数等于从该结点出发所能到达的结点（包括自身在内）的个数，赋给fa的数作为f（a），赋给ga的数作为g（a）。

如果存在环路

则有f（a）＞g（b）≥f（c）≥…≥f（x）≥g（y）＞f（a），从而导致f（a）＞f（a）而产生矛盾。

例5.5 利用关系图法给出表5-4的优先关系表所对应的优先函数。

表5-4所示优先关系表对应的关系图如图5-5所示，从该图所得的函数f和g如表5-6所示。

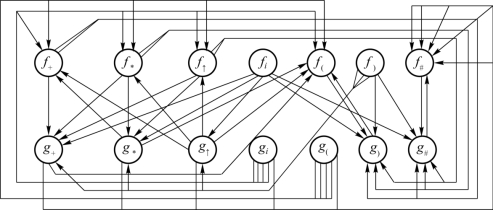
图5-5　表5-4的优先关系表对应的优先关系图

表5-6　表5-4的优先关系表对应的优先函数表

2.逐次加1法

有向图法可以在确定的步数内完成优先函数的构造。但是，当结点数目比较多时，有向图会变得十分复杂，可能难于统计每个结点所能到达的结点个数。另一种构造优先函数的方法称为逐次加1法。逐次加1法是一个迭代的过程，需要多次重复，算法才能够得到收敛。逐次加1法优先函数构造的步骤如下：

（1）初始化，对所有终结符a，f（a）=g（a）=1(www.xing528.com)

（2）对于a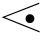b，如果f（a）≥g（b），则设g（b）=f（a）+1

（3）对于ab，如果f（a）≤g（b），则设f（a）=g（b）+1

（4）对于ab，如果f（a）≠g（b），则设f（a）=g（b）=max（f（a），g（b））

重复步骤（2）～（4），直至得到的f和g的数值不再变化，过程得到收敛。如果f和g的数值大于2n（n是文法终结符的个数），则表明对应的优先函数不存在，过程无法收敛。

例5.6 利用逐次加1法求表5-4所示优先关系表对应的优先函数。

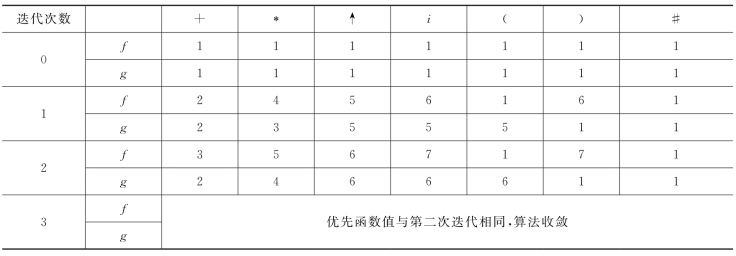
利用逐步加1法求取表5-4所示优先关系表对应的优先函数的迭代过程，以及所得的函数f和g如表5-7所示。

表5-7　优先函数表

虽然实现容易，但优先函数有一个缺点，就是原本不存在优先关系的两个终结符，由于与自然数相对应而变成可比较的了，这样可能会掩盖输入串中的错误。但可以通过检查栈顶符号θ和输入符号a的具体内容来发现那些不可比较优先关系的情形。此外，也有许多优先关系表不存在对应的优先函数。

例5.7 利用关系图法给出表5-8中优先关系表所对应的优先函数。

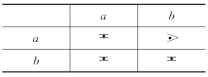
表5-8给出的优先关系表实际上不存在优先函数。因为，假定存在f和g，则应有

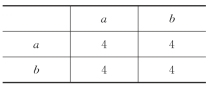
表5-8　优先关系表

f(a)=g(a),f(a)＞g(b)

f(b)=g(a),f(b)=g(b)

从而导致矛盾

f(a)＞g(b)=f(b)=g(a)=f(a)

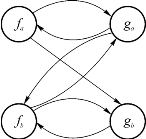
依据表5-8绘制的关系图如下图所示，图中含有环路。从依据关系图得到的优先函数表可以明显看出与终结符的优先关系与表5-8给出的优先关系是不相符的。