消除左递归方法-编译原理与实践

1.左递归文法

由上所述，递归定义的文法可以用于生成符号串重复形式的结构。但是左递归文法却无法构造确定的自上而下分析方法。

假定文法非终结符A的产生式为

A→Aα|β

其中，β的首字符不是A。这种形式的产生式称为直接左递归产生式。如果文法中至少含有一条左递归产生式，则称文法是左递归文法。

此外，考虑如下形式的文法

A→Bα|β

B→Aγ|δ

消除左递归

文法中不含有任何直接左递归产生式。但是，利用文法推导符号串的过程中，可能存在类似A⇒Bα⇒Aγα的推导过程，出现了间接的左递归形式，也将面临直接左递归相同的问题。因此，存在AA…推导形式的文法也是左递归文法。

2.消除直接左递归

文法的左递归可以通过产生式的形式变换而消去。直接左递归形式的产生式A→Aα|β，通过引入新的非终结符A，可以改写为

A→βA

A→αA|ε

改写后的文法与原文法具有不同的形式，不包含直接左递归。但是，两个文法的语言是等价的。也就是说，两种文法能够推出的符号串是相同的。

例4.3 消除算术表达式文法的左递归

通过观察可以发现，非终结符E和T的产生式中含有直接左递归。依据消除左递归的文法变换规则，消去直接左递归后的表达式文法为

一般而言，假设文法中非终结符A的全部产生式为

A→Aα1|Aα2|…|Aαm|β1|β2|…|βn|

其中，βi的首字符都不是A，可将产生式改写为

A→β1A|β2A|…|βnA

A→α1A|α2A|…|αmA|ε

从而消除关于A的直接左递归。

表达式文法的左递归性

根据表达式的定义，表达式文法的基本形式为

E→E+E|E*E|(E)|i

这个文法由于无法处理运算符之间的优先关系而具有二义性。

通过将相同优先级别的运算符归纳在一组中，可以描述运算符之间的优先级别。因此，可以将优先级别高的乘法与优先级别低的加法进行分组，得到如下文法

其中，加法被归在非终结符E的规则中，而乘法被归在非终结符T的规则中，更高优先级别的括号运算被归在非终结符F的规则中。这样，在构造语法分析树时，乘法运算将作为加法运算的操作数而进行分组。或者说，语法树中加法将比乘法更靠近树的根结点，具有更低的优先级别，如图4-3所示。

图4-3　表达式文法（G4.3）包含的优先关系

但是，上述文法仍然具有二义性，原因是文法无法描述相同优先级别运算符的结合性，如图4-4所示。为了满足数学算术运算的左结合性，需要强制产生式从左侧产生相同优先级别的运算符号。因此，算术表达式采用左递归形式的文法（G4.1）。

图4-4　表达式文法（G4.3）具有二义性

左递归文法无法建立确定的自上而下的语法分析，那么将文法改为如下右递归形式的文法可以吗？右递归文法与左递归文法的形式基本类似，并且具有相同的语言集合。但是，利用两个文法为相同的输入串构建语法分析树将发现，左递归文法使得相同优先级别的运算符具有左结合性，而右递归文法使得运算符具有了右结合性，如图4-5所示。(www.xing528.com)

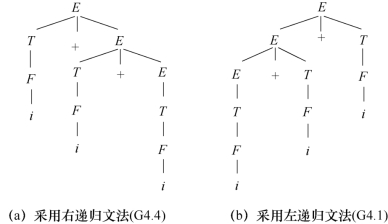
图4-5　表达式i+i+i的语法分析树

3.消除所有左递归

考虑文法

文法虽然不含有直接左递归，但是存在类似S⇒Qc⇒Rbc⇒Sabc的推导，因此，S、Q、R都是间接左递归的。上述通过产生式形式变换的方法，无法消除多步推导而产生的间接左递归。那么，如何消除一个文法的一切左递归？

如果一个文法不存在循环或ε产生式，执行算法4.1能保证消除所有左递归。其中，循环是指推导中出现了以相同非终结符开始和结束的推导过程，即形如A⇒*A的推导。循环将导致分析程序进入无穷循环，因此带有循环的文法不会作为程序设计语言的文法出现；ε产生式是形如A→ε的产生式，程序设计语言的文法中确实存在ε产生式，但是通常都是在有限的情形中，因此算法对于大多数文法都是有效的。

算法4.1的基本思想是通过代入的方式，使得经过若干步推导才会展现出来的左递归显式地呈现于产生式中。例如，对不含有直接左递归形式的产生式

A→Bα|β

B→Aγ|δ

将B代入A的含义是，利用B的产生式的右部，替换A的产生式右部中的B，于是可得

A→Aγα|δα|β

将隐藏在产生式中的左递归表示为直接左递归的形式。

代入实质上是将非终结符经过推导后的形式直接呈现于产生式中。需要注意，只有通过代入有可能产生左递归的情形下，才进行代入动作。换句话说，只有B出现在A的产生式右部的最左端，将B的右部代入A的右部后才有可能展现出潜在的左递归。如果在其他位置进行代入，只是增加了产生式右部符号串的长度，不可能出现直接左递归。此外，代入还必须遵循一定的顺序，不能将B代入A后，又试图将A代入B，这样将无法停止代入动作。

算法4.1 消除文法的全部左递归

（1）将文法G的所有非终结符按任意一种顺序排列成A1，A2，…，An；

(2)for(i=1;i=n;i++)

（3）化简（2）所得的文法，即删除从开始符号出发无法到达的非终结符的产生式。

例4.4 消除文法（G4.5）的左递归。

第1步，将非终结符排序为R、Q、S。

第2步，考察R，R不含直接左递归，将R代入到Q的有关候选式，Q的产生式变为

Q→Sab|ab|b

第3步，Q的产生式不含直接左递归。将R和Q分别代入S的有关候选式（R无法代入）后，S的产生式变为

S→Sabc|abc|bc|c

第4步，消除S的直接左递归后，最终的文法为

S→abcS|bcS|cS

S→abcS|ε

Q→Sab|ab|b

R→Sa|a

显然，由S出发进行推导时，将无法遇见非终结符Q和R，因此关于Q和R的产生式是多余的。经化简后所得的文法是

注意，由于对非终结符排序的不同，最后所得的文法在形式上可能不一样。但不难证明，它们都是等价的。例如，若对文法（G4.5）的非终结符排序选为S、Q、R，那么，最后所得的无左递归，并且与文法（G4.6）等价的文法为

S→Qc|c

Q→Rb|b

R→bcaR|caR|aR

R→bcaR|ε