编译原理与实践：自上而下分析方法

从推导的角度看，自上而下分析过程实质上是不断建立直接推导的过程。如果采用最左推导方式，那么分析的每一步都是以当前句型中最左边的非终结符产生式的右部符号串，替换这个非终结符而生成新的句型。或者说，是对非终结符号进行展开，生成语法分析树下一层分支的过程。

文法中的非终结符号可能具有多个候选式，这种情况下，推导过程中将难以确定应该使用哪个候选式完成展开动作。因此，自上而下的分析可能产生一定的试探过程。

例4.1 判断输入串w=a*b是否为如下文法的句子

S→a Ab

A→**|*

自上而下语法分析举例

动画：自上而下语法分析过程实例

依据文法自上而下地为输入串w构造语法分析树时，首先由文法的开始符号S出发，选择其唯一的候选式，展开语法树的第一层子结点。此时，输入符号‘a’得到了匹配，如图4-1左侧子树所示。输入串的扫描指针将向右移动到下一个输入符号‘*’。

然后，利用句型中最左侧的非终结符A进行推导时，发现A具有两个候选式。如果采用简单的策略，可以指定利用A的第一个候选式A→**进行推导，如图4-1中间子树所示，当前输入符号‘*’得到了匹配。但是，扫描指针向右移动到下一个输入符号‘b’，与语法树叶子结点中的第二个‘*’不匹配。此时，需要重新选用A的另一个产生式A→*进行推导尝试，如图4-1右侧最终语法树所示。在这种尝试下，输入串中后续符号都能够得到匹配，从而完成了为w构造语法树的任务，证明了w是一个句子。

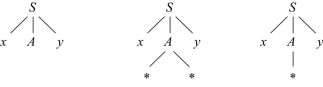
图4-1　不确定的自上而下语法分析(www.xing528.com)

通过上面的例子可以看出，自上而下分析过程是一种通过使用非终结符号不同的候选式，试探地匹配输入串的过程。每当某个选择匹配失败时，就需要撤销所构造的失败分支，从而选取另一个候选再次进行尝试，这一过程称为回溯。

除了上述情形将产生回溯，有一种特殊形式的文法将使得自上而下分析过程陷入循环中。

例4.2 判断输入串w=baaa是否为如下文法的句子

S→Sa

S→b

自上而下为输入串w构建语法分析树将以文法的开始符号S作为根结点。由于输入串的第一个符号为‘b’，为与‘b’匹配则应选用S→b来进行推导。但是，这样将无法推导出w后边的部分，如图4-2的第一棵子树所示。通过回溯采用S→Sa推导时，却无法确定什么时候应该采用S→b进行推导，从而出现图4-2所示的后续多次回溯的情况。

图4-2　包含循环的语法分析过程

例4.2中，利用S进行推导时，在没有识别出任何输入符号的情况下，又因为重新要求S进行新的匹配而产生了循环。上述文法在生成语句时出现的循环试探过程，是由于文法中存在特殊形式的产生式，其左部符号与右部的第一个符号相同。这种递归定义的非终结符在匹配输入时，只有经过若干次递归选择后，才能选择递归终止产生式。由于递归定义出现在产生式右部的第一个位置，或者说左端，因此产生式称为左递归产生式。

带有回溯的自上而下分析是一个穷举式的试探过程，当分析不成功时则推翻当前的分析，并退回到适当位置，再重新试探其余候选进行推导。通过记录已使用过的产生式，直到将所有可能的推导序列都测试完成仍不成功时，才会确认输入串不是文法的句子。

回溯分析功能强大，任何上下文无关文法都可以通过这种方法进行识别。但是，在编译程序真正实现时，往往是边进行语法分析边插入语义动作，完成语义分析，因而带有回溯的分析代价很高、效率很低，在实用编译程序中几乎不使用这种方法。虽然非确定的分析方式并不实用，但它却展示了编译程序的许多特性。

通过对文法进行限制可以避免回溯，构造确定的自上而下分析过程。虽然，不是每一个上下文无关文法都能构造一个确定的自上而下分析器，但是能用确定的自上而下分析方法进行分析的上下文无关文法，有充分的能力定义大多数常用的高级程序设计语言，用以构造有效的编译程序。