不仅正规文法和有限自动机是等价的,正规式和有限自动机也是等价的,即,由正规式所描述的语言和有限自动机所识别的语言相同。其等价性体现在以下两个方面:
(1)对任何有限自动机M,都存在一个正规式r,使得L(r)=L(M);
(2)对任何正规式r,都存在一个有限自动机M,使得L(M)=L(r)。
1.不确定有限自动机转换为正规式
对于Σ上的NFA M,令每条弧可用一个正规式来标记,以此来构造Σ上的正规式r,使得L(r)=L(M)。步骤如下:

正则表达式到有限自动机
首先,在M的状态转换图上加入两个结点,一个为X,另一个为Y。从X用ε弧连接到M的所有初态结点,从M的所有终态结点用ε弧连接到Y,从而形成一个新的NFA,记为M,它只含一个初态结点X和一个终态结点Y。显然有,L(M)=L(M),即,这两个NFA是等价的。
其次,逐步消去M中的所有结点,直到仅剩下X和Y为止。在消除过程中,逐步用正规式来标记箭弧。消弧过程很直观,只需反复使用图3-15中的替换规则即可。
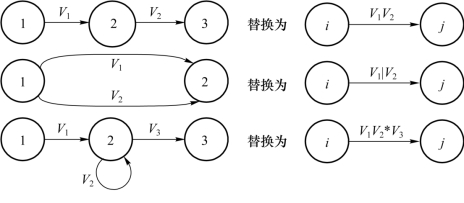
图3-15 替换规则
最后,从结点X到Y的弧上的标记即可得到所求的正规式r。
例3.8 图3-16(a)给出了一个NFA M,下面将求出与之等价的正规式r。
首先,如图3-16(b)所示,加入结点X和Y,形成一个新的NFA M;然后,利用替换规则逐步消去M中的结点,直到仅剩下X和Y为止,如图3-16(c)所示;最后,从X和Y之间弧上的标记可以看出,r=(a|b)(a|b)*。

图3-16 由NFA构造正规式
2.正规式转换为不确定有限自动机
从Σ上的一个正规式r构造Σ上的NFA M,其基本思想介绍如下:
首先分析r,将其分解成子表达式,然后使用下面的规则(1)至(3),为r中的每个基本符号(ε或字母表符号)构造NFA。基本符号对应正规式定义的(1)和(2)两部分。若符号a在r中多次出现,则为其每次出现都要构造NFA。
然后,据r的语法结构,使用下述规则(4)将这些NFA归纳组合起来,直至获得整个正规式的NFA为止。构造过程中所产生的中间NFA具有如下性质:①只有一个终态;②没有弧进入开始状态;③没有弧离开终态。在下面的NFA中,x是初始状态,y是接受状态。

由正则表达式到NFA
(1)对正规式φ构造NFA,如图3-17(a)所示。
(2)对于ε构造NFA,如图3-17(b)所示。显然,它识别{ε}。(https://www.xing528.com)
(3)对Σ中的每个符号a构造NFA,如图3-17(c)所示,它识别{a}。

图3-17 识别正规式φ、ε和a的NFA
(4)如果N(s)和N(t)分别是正规式s和t的NFA,则:
①如图3-18所示,对正规式s|t构造合成的NFA N(s|t)。加入结点x和y,从x引ε弧到N(s)和N(t)的初始状态,从N(s)和N(t)的接受状态引ε弧到结点y。N(s)和N(t)的初始和接受状态不再是N(s|t)的初始和接受状态。这样,从x到y的任何路径必须独立完整地通过N(s)或N(t)。可以看出,该合成的NFA能够识别L(s)∪L(t)。
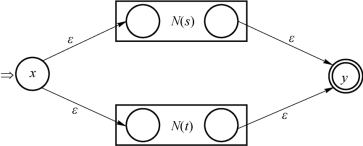
图3-18 识别正规式s|t的NFA
②如图3-19所示,对正规式st构造合成的NFA N(st)。N(s)的初始状态成为合成后的NFA的初始状态,N(t)的接受状态成为合成后的NFA的接受状态,N(s)的接受状态和N(t)的初始状态合并,且合并后的这个状态不作为合成后的NFA的接受状态或开始状态。从x到y的路径必须首先经过N(s),再经过N(t),该路径上的标记拼成L(s)L(t)中的串。由于没有边进入N(t)的初始状态或离开N(s)的接受状态,因此,在x到y的路径中不存在N(t)回到N(s)的现象,所以,合成后的NFA能够识别L(s)L(t)。
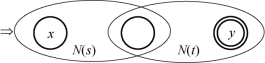
图3-19 识别正规式st的NFA
③如图3-20所示,对正规式s*构造合成的NFA N(s*)。同样,x和y分别是新的初始状态和接受状态。在此合成的NFA中,可以沿ε边直接从x到y,这意味着ε∈L(s*);也可以从x经过N(s)一次或多次。很明显,该NFA能够识别L(s*)。
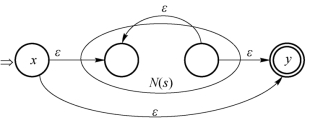
图3-20 识别正规式s*的NFA
④对于括起来的正规式(s),则使用N(s)本身作为其NFA。
需要注意的是,对每次构造的新状态都要赋予不同的名字,从而使得所有的状态名都不相同。
例3.9 构造与正规式r=01*|1等价的有限自动机。首先,将r分解为最基本的子表达式1和0,接着按如下步骤进行:
(1)如图3-21(a)所示,构造与正规式1和0等价的有限自动机;
(2)如图3-21(b)所示,构造与1*等价的有限自动机;
(3)如图3-21(c)所示,将0和1*的有限自动机连接,构造与01*等价的有限自动机;
(4)如图3-21(d)所示,将01*和1的有限自动机合并,构造与01*|1等价的有限自动机。
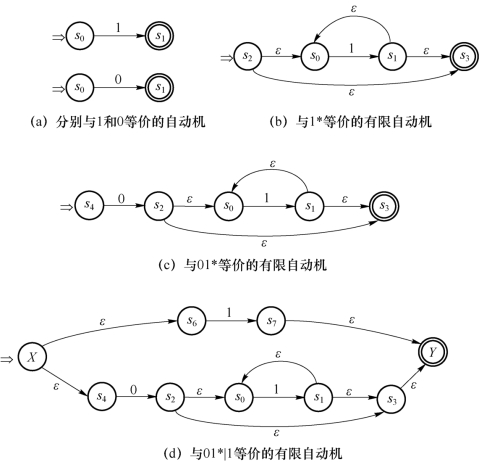
图3-21 与正规式r等价的有限自动机的构造过程
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




